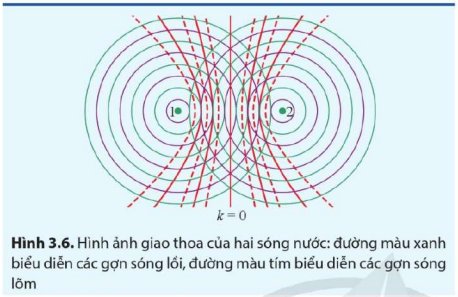
Dùng bút chì vẽ đường nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng trên Hình 3.6 và đối chiếu kết quả với công thức (3.1).
\(x_1-x_2=k\lambda\) (k là số nguyên) (3.1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
8 tháng 9 2019
Đáp án A
Các vị trí gợn lồi gặp gợn lồi → cực đại giao thoa, ngược lại các vị trí gợn lõm gặp gợn lõm là cực tiểu giao thoa
VT
30 tháng 7 2017
Đáp án A
+ Các vị trí gợn lồi gặp gợn lồi → cực đại giao thoa, ngược lại các vị trí gợn lõm gặp gợn lõm là cực tiểu giao thoa
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Tham khảo:
- Cách xác định bước sóng do hai nguồn phát ra:
+ Đo khoảng cách giữa hai nguồn.
+ Đếm số khoảng cách giữa đỉnh hai gợn lồi liên tiếp hoặc số khoảng cách giữa đỉnh hai gợn lõm liên tiếp do hai nguồn tạo ra.
+ Dựa vào khái niệm bước sóng là khoảng cách gần nhau nhất giữa hai gợn lồi hoặc hai gợn lõm.
- Áp dụng:
+ Giả sử đối với hình 3.6 ở trên ta đo được khoảng cách giữa hai nguồn S1S2 = a
+ Khoảng giữa hai nguồn có 4 gợn lồi (không tính 2 nguồn) bằng 3.
Khi đó hoàn toàn tính được bước sóng \(\lambda=\dfrac{a}{3}\)
VT
11 tháng 10 2017
Đáp án: A
HD Giải:
Ta có: khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là 2cm → λ/2 = 2 → λ = 4cm
Hai nguồn ngược pha, nên điểm dao động với biên độ cực đại phải thỏa mãn: d2 – d1 = (k + 0,5)λ
Điểm dao động với biên độ cực tiểu thỏa mãn: d2 – d1 = k.λ
Số gợn lồi và lõm xuất hiện giữa hai điểm S1S2 là:
<=> 
<=> 
10 tháng 11 2015
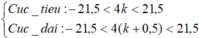
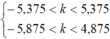
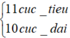
Khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là \(\frac{\lambda}{2} \Rightarrow \lambda = 2.2=4cm\)
Số gợn lồi (dao động cực đại) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< k \lambda < S_{1}S_{2}\Rightarrow -4.125 < k < 4.125\\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3,4\)
=> có 9 gợn lồi.
Số gợn lõm (dao động cực tiểu) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< (k+0.5) \lambda < S_{1}S_{2}\Rightarrow -4.125 < k+0.5 < 4.125\\ \Rightarrow -4.625 < k < 3.625 \\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3.\)
=> có 8 gợn lõm.
VT
18 tháng 9 2018
Đáp án A
Bước sóng chín
h bằng hai gơn lồi liên tiếp: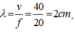 
.
*Do tính chất đối xứng hai gợn lồi liên tiếp (tính từ cần rung) có đường kính chênh lệch nhau 
.
Nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng với mỗi nguồn, đo khoảng cách \(x_1,x_2\). Tính \(\dfrac{x_1-x_2}{\lambda}\) với \(\lambda\) được xác định trong câu hỏi trước. Nếu thương số nhận được là một số nguyên thì kết quả đúng với công thức.