a) Trong không gian, cho điểm \(M\) ở ngoài đường thẳng \(d\). Đặt \(\left( P \right) = mp\left( {M,d} \right)\). Trong \(\left( P \right)\), qua \(M\) vẽ đường thẳng \(d'\) song song với \(d\), đặt \(\left( Q \right) = mp\left( {d,d'} \right)\). Có thể khẳng định hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau không?
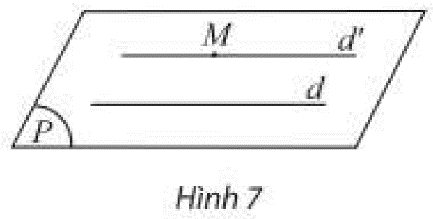
b) Cho ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) cắt nhau theo ba giao tuyến \(a,b,c\) phân biệt với \(a = \left( P \right) \cap \left( R \right);b = \left( Q \right) \cap \left( R \right);c = \left( P \right) \cap \left( Q \right)\) (Hình 8).
Nếu \(a\) và \(b\) có điểm chung \(M\) thì điểm \(M\) có thuộc \(c\) không?
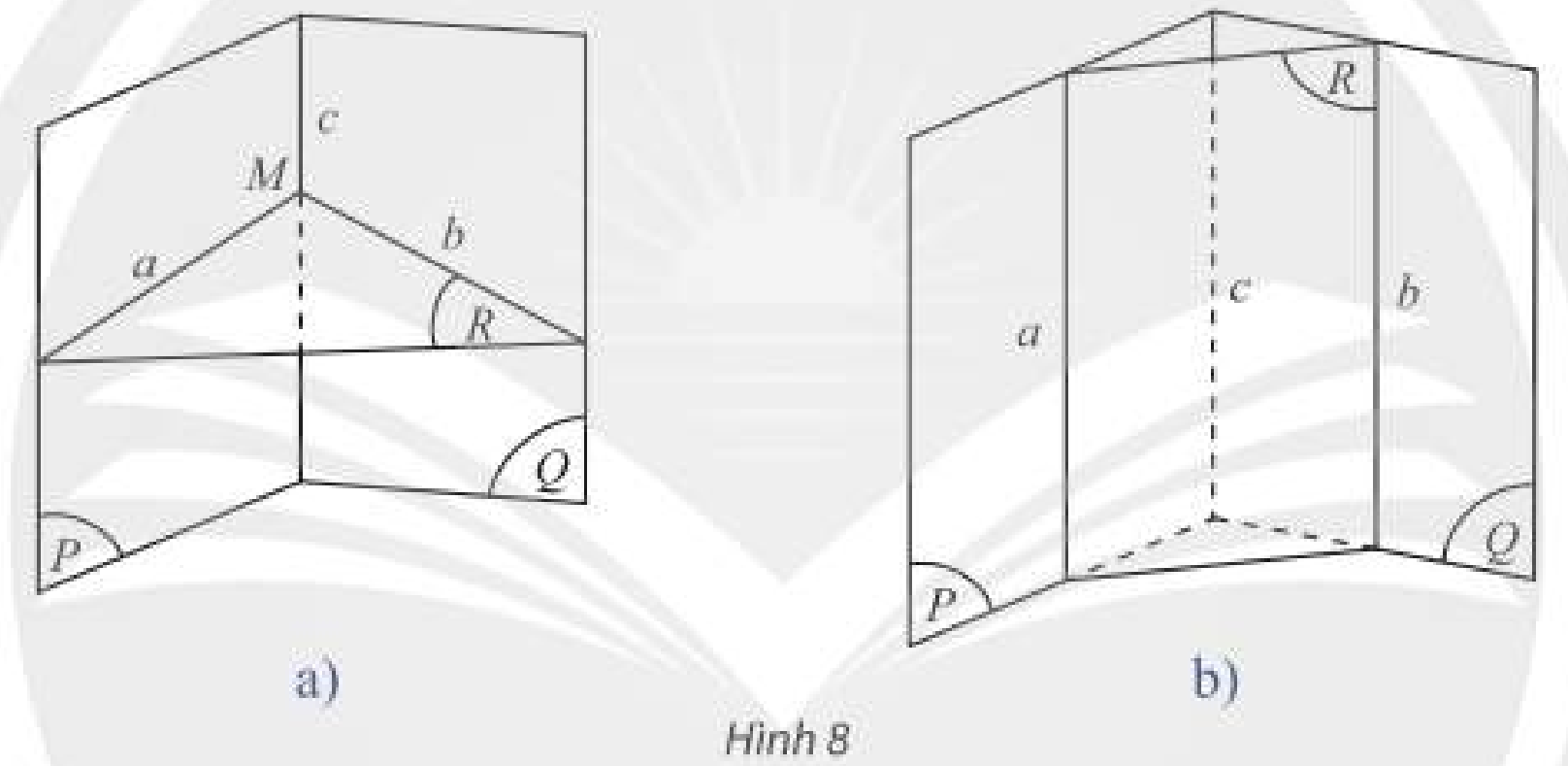

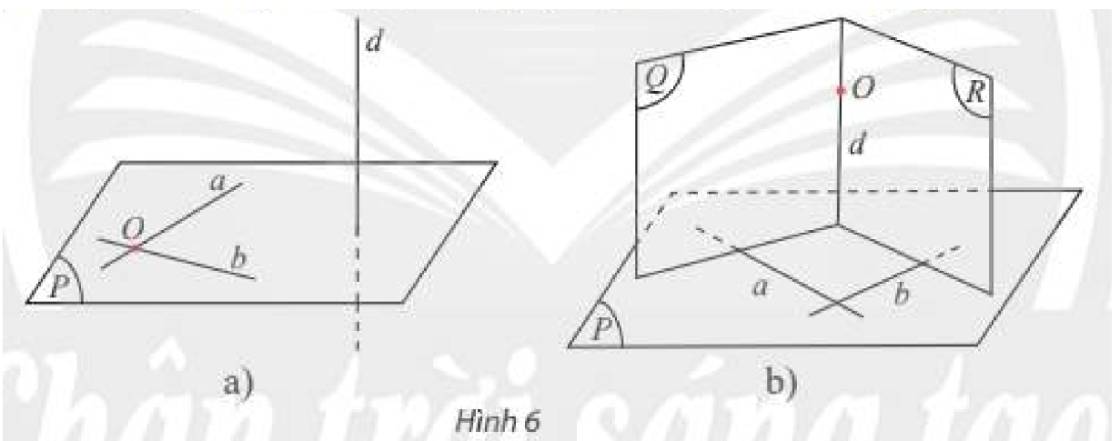



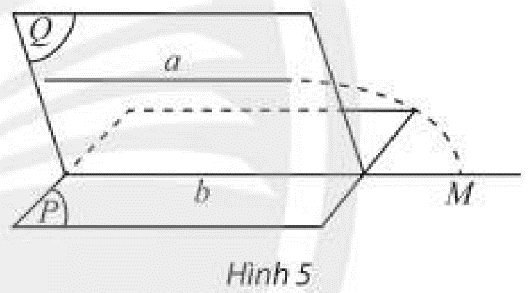

a) Theo đề bài ta có: \(d' \subset \left( P \right),d' \subset \left( Q \right)\) nên \(d'\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Lại có: \(d \subset \left( P \right),d \subset \left( Q \right)\) nên \(d\) cũng là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Theo tính chất thừa nhận 5: hai mặt phẳng phân biệt có một đường thẳng chung duy nhất. Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in a\\a \subset \left( P \right)\end{array} \right\} \Rightarrow M \in \left( P \right)\\\left. \begin{array}{l}M \in b\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\end{array}\)
Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in c\).