Cho hình thoi ABCD có \(\widehat {C{\rm{D}}B} = {40^o}\). Tính số đo mỗi góc của hình thoi ABCD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
ABCD là hình thoi nên AB = BC = CD = DA ( = CA = 4 cm)
Do đó: tam giác ABC là tam giác đều ( do AB = BC = CA ( = 4 cm))
Suy ra, góc B = 60o
Mà góc B và góc D là hai góc đối nhau nên theo tính chất hình thoi, góc D = 60o
------------------------------------
Theo tính chất hình thoi, 2 đường chéo vuông góc với nhau nên AC vuông góc với BD tại O
Tam giác đều ABC có OB là đường cao nên cũng là đường trung tuyến
Do đó: \(OA=OC=\frac{1}{2}.AC=\frac{1}{2}.4=2\) (cm)
Áp đụng định lý Py-ta-go vào tam giác OAB, ta được:
\(AB^2=OA^2+OB^2\)
\(\Rightarrow\) \(OB^2=AB^2-OA^2=4^2-2^2=16-4=12\)
\(\Rightarrow\) \(OB=\sqrt{12}\) (cm)

THAM KHẢO:

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)



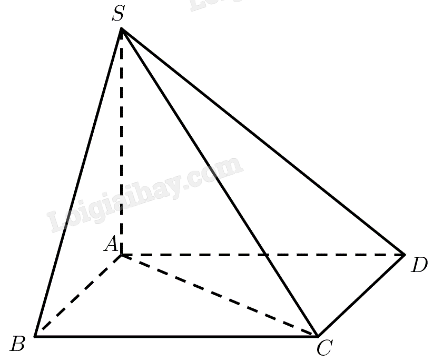
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(AB = BC = AC = a \Rightarrow \Delta ABC\) đều \( \Rightarrow \widehat {BA{\rm{C}}} = \widehat {ABC} = {60^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({60^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình thoi \( \Rightarrow \widehat {BA{\rm{D}}} = {180^ \circ } - \widehat {ABC} = {180^ \circ } - {60^ \circ } = {120^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({120^ \circ }\).
c) \(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = {45^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^ \circ }\).

tihs chất hình thoi là 2 goc đối bằng nhau
Do C là góc đối của A mà A = 40 độ nên C = 40 độ
2 goc B và D cũng dối nhau nên bằng nhau
góc B cộng D = 360 - 40 - 40 = 280độ
=> B=D = 280:2=140 độ

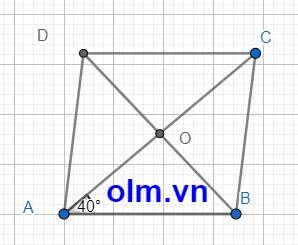
Vì ABCD là hình thoi nên ⇒ tam giác ABD cân tại A
Vì O là trung điểm DB nên AO là truyến là đường phân giác của tam giác ABD
⇒ \(\widehat{DAO}\) = 400
⇒ \(\widehat{DAB}\) = 400 + 400 = 1800
⇒ \(\widehat{ADC}\) = 1800 - 800 = 1000
⇒ \(\widehat{DCB}\) = 1800 - 1000 = 800
\(\Rightarrow\) \(\widehat{ABC}\) = 1800 - 800 = 1000
Do ABCD là hình thoi nên DB là tia phân giác của \(\widehat {CDA}\)
Mà: \(\widehat {CDB} = {40^0} \Rightarrow \widehat {CDA} = {2.40^0} = {80^0} \Rightarrow \widehat {CBA} = \widehat {CDA} = {80^0}\)
Mặt khác:
\(\begin{array}{l}\widehat {BAD} + \widehat {CBA} + \widehat {CDA} + \widehat {BCD} = {360^0}\\\widehat {BAD} + {80^0} + {80^0} + \widehat {BCD} = {360^0}\end{array}\)
(do ABCD là hình thoi nên \(\widehat {BAD} = \widehat {BCD}\))
\( \Rightarrow \widehat {BAD} = \widehat {BCD} = \frac{{{{360}^0} - {{80}^0} - {{80}^0}}}{2} = {100^0}\)
Vậy hình thoi ABCD có: \(\widehat {BCA} = \widehat {CDA} = {80^0};\widehat {BAD} = \widehat {BCD} = {100^0}\)