\(\frac{-2002}{2003}\) và \(\frac{2005}{-2004}\)
So sánh các số hữu tỉ sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1) Áp dụng BĐT \(\frac{a}{b}>\frac{a-m}{b-m}\) với \(\frac{a}{b}< 1\) .Dễ dàng chứng minh Bđt trên, áp dụng vào ta có:
a) \(x=\frac{2002}{2003}=\frac{2002-1+1}{2003-1+1}=\frac{2003-1}{2004-1}< \frac{2003}{2004}\)
Với \(\frac{a}{b}=\frac{2003}{2004};\frac{a-m}{b-m}=\frac{2003-1}{2004-1}\)
Từ đó ta có: x < y
b) Vì đây là phân số âm nên bé hơn phân số dương nên ta có BĐT: \(\frac{a}{b}>\frac{c}{d}\Leftrightarrow\frac{-a}{b}< \frac{-c}{d}\)
Áp dụng vào bài toán trên với \(\frac{a}{b}=\frac{2002}{2003}< 1\)và \(\frac{c}{d}=\frac{2005}{2004}>1\)
Nên \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow\frac{-a}{b}>\frac{-c}{d}\)hay x > y
Bài 1 :
a, Ta có : \(x=\frac{2002}{2003}=1-\frac{1}{2003}\)
\(y=\frac{2003}{2004}=1-\frac{1}{2004}\)
Vì \(\frac{1}{2003}>\frac{1}{2004}\)
\(\Rightarrow1-\frac{1}{2003}< 1-\frac{1}{2004}\)
\(\Rightarrow x< y\)
b, Ta thấy cả 2 vế đều có dấu âm nên ta rút gọn dấu âm đi thì được :
\(x=\frac{2002}{2003}\) \(y=\frac{2005}{2004}\)
Lúc này :
Ta có : \(y=\frac{2005}{2004}>1=\frac{2003}{2003}>\frac{2002}{2003}=x\)
Vì khi so sánh dương sẽ đối ngược với so sánh âm :
\(\Rightarrow\)Khi trả lại dấu âm thì tất nhiên \(x=\frac{-2002}{2003}>y=\frac{2005}{-2004}\)
Vậy \(x>y\)
Bài 2 :
Ta quy đồng các phân số trên như sau :
\(\frac{-2}{7}=\frac{-6}{21}\) \(\frac{-2}{9}=\frac{-6}{27}\)
Gọi các phân số thỏa mãn điều kiện trên là x .
Ta có : \(\frac{-6}{21}< x< \frac{-6}{27}\)
\(\Rightarrow x\in\left\{\frac{-6}{22};\frac{-6}{23};\frac{-6}{24};\frac{-6}{25};\frac{-6}{26}\right\}\)
Ta rút gọn và dấu của các phân số như sau ( nếu không rút gọn được thì cúng đừng chuyển dấu ) :
\(x\in\left\{\frac{3}{-11};\frac{-6}{23};\frac{3}{-12};\frac{-6}{25};\frac{3}{-13}\right\}\)
Vậy các phân số thỏa mãn đề bài là : \(\frac{3}{-11};\frac{3}{-12};\frac{3}{-13}\).

mỗi số hạng trong biểu thức A đều nhỏ hơn 1 mà có 15 số nên tổng A sẽ nhỏ hơn 15
ta thay tong tren <1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
hay tong tren be hon 15

a.\(\frac{13}{17}\)=1-\(\frac{4}{17}\); \(\frac{46}{50}\)=1-\(\frac{4}{50}\)
Vì \(\frac{4}{17}\)>\(\frac{4}{50}\)=> 1-\(\frac{4}{17}\)<1-\(\frac{4}{50}\)
Vậy\(\frac{13}{17}\)<\(\frac{46}{50}\)

a) ta thay 1-2002/2003= 1/2003 va 1-2003/2004=1/2004
ma 1/2003>1/2004 =>2002/2003<2003/2004
b) ta co -2002/2003<1<2005/2004

=1+1/2001+1+1/2002+1+1/2003+...+1+1/2008=8+1/2001+1/2002+1/2003+...+1/2008>8
\(\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>8\)

a) Ta có: \(1-\frac{2002}{2003}=\frac{1}{2003}\)
\(1-\frac{2003}{2004}=\frac{1}{2004}\)
Vì \(\frac{1}{2003}>\frac{1}{2004}\)
\(\Rightarrow\frac{2002}{2003}>\frac{2003}{2004}\)
b) Ta có: \(\frac{-2005}{-2004}=\frac{2005}{2004}>1\)
\(\frac{-2002}{2003}

Ta có :
\(\frac{-2002}{2003}>-1\)
\(-1>\frac{-2005}{2004}\)
\(\Rightarrow\frac{-2002}{2003}>\frac{-2005}{2004}\)
Ta có:
\(-\frac{2002}{2003}>-1\)
\(-\frac{2005}{2004}< -1\)
=> \(-\frac{2002}{2003}>-\frac{2005}{2004}\)
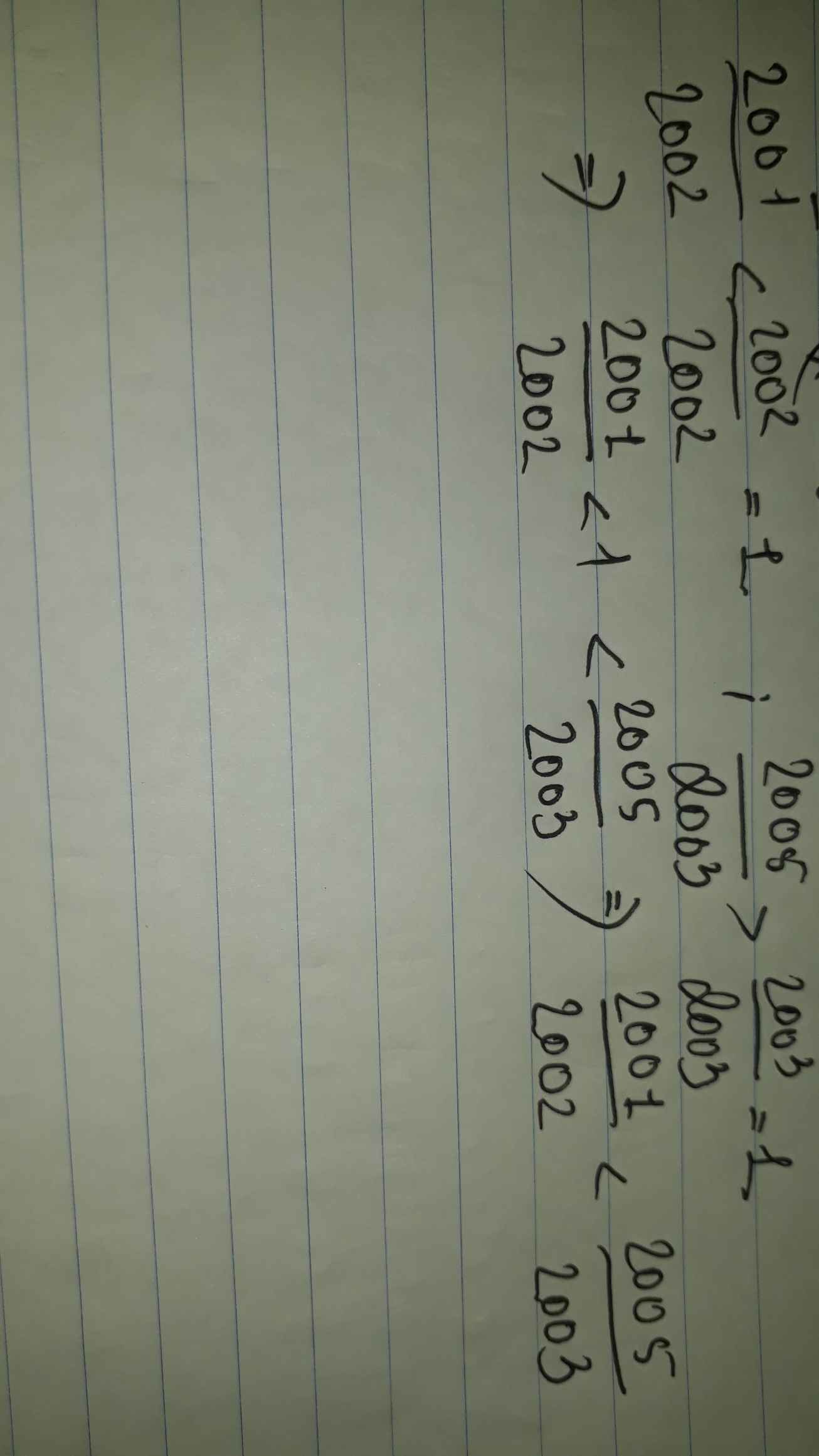
ta có
\(-\frac{2002}{2003}>-1>\frac{2005}{-2004}.\)
\(\Rightarrow-\frac{2002}{2003}>\frac{2005}{-2004}\)
\(\frac{2002}{2003}\)>\(\frac{2005}{-2004}\)