Quan sát hình chóp tứ giác đều ở Hình 3 và cho biết:
a) Mặt đáy và các mặt bên của hình đó.
b) Độ dài cạnh IB
và cạnh BC
c) Đoạn thẳng nào là đường cao của hình đó

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đỉnh: \(M\)
Mặt đáy: \(ABC\)
Các mặt bên: \(MAB\); \(MAC\); \(MBC\)
b) Các cạnh bên bằng nhau: \(MA = MC = 17\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 13\)cm
c) Đoạn thẳng \(MO\) là đường cao của hình chóp tam giác đều \(M.ABC\)

Hình chóp tứ giác đều \(S.MNPQ\) có:
a) Mặt bên: \(SMN\); \(SNP\); \(SPQ\); \(SMQ\)
Mặt đáy: \(MNPQ\)
b) Các cạnh bên bằng nhau: \(SM = SN = SP = SQ = 15\)cm
Các cạnh đáy bằng nhau: \(MN = NP = PQ = MQ = 8\)cm

- Mặt bên: \(MAB\), \(MAC\), \(MBC\)
- Mặt đáy: \(ABC\)
- Đường cao: \(MO\)
- Độ dài cạnh bên: \(15\)cm
- Độ dài cạnh đáy: \(10\)cm

Hình chóp tam giác đều \(S.DEF\) có:
a) Mặt bên: \(SDE\); \(SDF\); \(SEF\)
Mặt đáy: \(DEF\)
b) Các cạnh bên bằng nhau: \(SE = SF = SD = 5\)cm
Các cạnh đáy bằng nhau: \(ED = EF = DF = 3\)cm
c) Đáy \(DEF\) là tam giác đều nên ba góc ở đáy bằng nhau và bằng \(60^\circ \)

| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |

Các mặt bên là MAB, MAC, MBC
Các cạnh bên là MA = MB = MC = 15cm
Đường cao là MO
Các cạnh đáy là AB = AC = BC =10cm

Chọn A
Phương pháp:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải


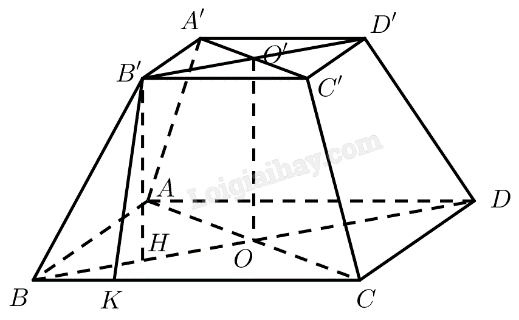
Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy.
Kẻ \(B'H \bot B{\rm{D}}\left( {H \in B{\rm{D}}} \right),B'K \bot BC\left( {K \in BC} \right)\)
\(\begin{array}{l}B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = 2a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = a\sqrt 2 \\B'D' = \sqrt {A'B{'^2} + A'{\rm{D}}{{\rm{'}}^2}} = a\sqrt 2 \Rightarrow B'O' = \frac{1}{2}B'{\rm{D'}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
\(OO'B'H\) là hình chữ nhật \( \Rightarrow OH = B'O' = \frac{{a\sqrt 2 }}{2},B'H = OO' = a\)
\( \Rightarrow BH = BO - OH = \frac{{a\sqrt 2 }}{2}\)
Tam giác \(BB'H\) vuông tại \(H\) có: \(BB' = \sqrt {B'{H^2} + B{H^2}} = \frac{{a\sqrt 6 }}{2}\)
\(BCC'B'\) là hình thang cân \( \Rightarrow BK = \frac{{BC - B'C'}}{2} = \frac{a}{2}\)
Tam giác \(BB'K\) vuông tại \(K\) có: \(B'K = \sqrt {BB{'^2} - B{K^2}} = \frac{{a\sqrt 5 }}{2}\)
a) Mặt đáy: \(ABCD\)
Các mặt bên: \(IAD\); \(IAB\); \(IBC\); \(ICD\)
b) Các cạnh bên bằng nhau: \(IB = IC = 18\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 14\)cm
c) Đoạn thẳng \(IH\) là đường cao của hình chóp