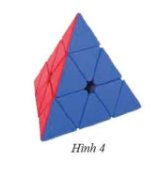
Tính thể tích khối rubik có dạng hình chóp tam giác đều (hình 4). Biết khối rubik này có bốn mặt là các tam giác đều bằng nhau cạnh \(4,7\)cm và chiều cao \(4,1\)cm; chiều cao của khối rubik bằng \(3,9\)cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích xung quanh của hình chóp tam giác đều là:
\(\frac{{99.40}}{2}.3 = 5940\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(\frac{{40.34,6}}{2} = 692\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(5940 + 692 = 6632\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.692.98,3 \approx 22674,53\) (\(c{m^3}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là:
\(\frac{{91.120}}{2}.4 = 21840\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(120.120 = 14400\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(21840 + 14400 = 36240\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.14400.68,4 = 328320\) (\(c{m^3}\))

a: Mặt đáy là tam giác đều cạnh 18cm
=>Chiều cao của tam giác đáy là \(18\cdot\dfrac{\sqrt{3}}{2}=9\sqrt{3}\left(cm\right)\)
b: \(V_1=\dfrac{1}{3}\cdot15\cdot\left(18^2\cdot\dfrac{\sqrt{3}}{4}\right)=5\cdot\dfrac{18^2}{4}\cdot\sqrt{3}=405\sqrt{3}\left(cm^3\right)\)
\(V_2=25\cdot30\cdot15=11250\left(cm^3\right)\)
\(\dfrac{V1}{V2}=\dfrac{405\sqrt{3}}{11250}=\dfrac{9}{250}\sqrt{3}\)

a) Vì 3 đỉnh của mặt màu đỏ đều nằm trên mặt bàn nên mặt màu đỏ cũng nằm trên mặt bàn.
b) Không thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn vì bốn đỉnh của rubik không cùng thuộc một mặt phẳng.
Trả lời câu hỏi: Có vô số mặt phẳng đi qua ba điểm thẳng hàng

a) Khối rubik tam giác có 4 đỉnh. Các đỉnh không cùng nằm trong một mặt phẳng
b) Khối rubik tam giác có 4 mặt. Mỗi mặt của khối rucik tam giác là những hình tam giác.
Diện tích đáy:
`(4.7 xx 4.1)/2 = 9,635 cm^2`.
Thể tích: `1/3 . 9,635 . 3,9 = 12,5255 cm^3`.