Sườn dốc dài là một mặt phẳng nghiêng góc 30độ với phương ngang. Khẩu pháo đặt trên đỉnh dốc bắn ra một viên đạn theo phương ngang với vận tốc đầu nòng 36 m / s . Bỏ qua sức cản không khí và lấy g =10 m / s2
a) Viên đạn rơi xuống sườn dốc ở vị trí cách đỉnh dốc bao xa và với vận tốc bao nhiêu?
b) Tính khoảng cách lớn nhất giữa viên đạn và mặt dốc trong quá trình đạn bay?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chọn gốc tọa độ là điểm ném O \(\equiv A\) ; chọn hệ trục tọa độ như hình vẽ , chiều dương hướng xuống , theo hướng ném
Phương trình tọa độ :
x = \(v_0.t\) ;
y = \(\dfrac{1}{2}gt^2=5t^2\)
Vì chiều dài đồi là L = 30m
nên chiều cao AH của đồi là \(AH=L.\sin30^{\text{o}}=15\left(m\right)\) ;
chiều dài đồi \(AB=L.\cos30^{\text{o}}=15\sqrt{3}\left(m\right)\)
Vì vật rơi trúng B nên \(x=AB=15\sqrt{3};y=AH=15\)
Giải hệ ta được \(v_0=15\left(m/s\right)\)
b) Chọn gốc O \(\equiv B\) tại vị trí ném , chọn hệ trục Oxy như hình vẽ,
chiều dương theo chiều Ox,Oy
Phương trình tọa độ :
\(x=v_0.\cos60^{\text{o}}.t=\dfrac{v_0.t}{2}\)
\(y=v_0.\sin60^{\text{o}}.t-\dfrac{1}{2}gt^2=\dfrac{\sqrt{3}v_0.t}{2}-5t^2\)
lại có \(AH=15\left(m\right);BH=15\sqrt{3}\left(m\right)\)
mà vật từ B rơi trúng A nên \(\left\{{}\begin{matrix}x=\dfrac{v_0t}{2}=15\sqrt{3}\\y=\dfrac{\sqrt{3}}{2}v_0t-5t^2=15\end{matrix}\right.\)
Giải hệ được \(v_0=15\sqrt{2}\left(m/s\right)\)
P/s : Sửa AB thành BH ở câu a

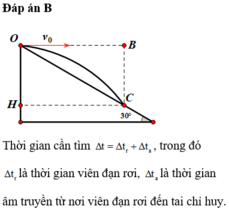
Đáp án B
Ta có x = 400 t , y = 5 t 2 ; khi viên đạn rơi vào sườn đồi ta có y x = tan 30 0 = 1 3

Lúc đầu hệ vật đứng yên có động lượng p 0 = 0. Ngay sau khi bắn, hệ vật có động lượng MV + mv = 0. Áp dụng định luật bảo toàn động lượng cho chuyển động theo phương ngang của hệ vật ta có:
p = p 0 ⇒ MV + mv = 0
suy ra MV = - mv hay V = -mv/M = -10.800/10000 = -0,8(m/s)

a) Thay g = 9,8 và \({v_0} = 500\)vào phương trình \(y = - \frac{g}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) ta được
\(\begin{array}{l}y = - \frac{{9,8}}{{{{2.500}^2}.{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \\ = - \frac{1}{{{{\cos }^2}\alpha }}{.1,96.10^{ - 5}}.{x^2} + x\tan \alpha \\ = - \left( {1 + {{\tan }^2}\alpha } \right){1,96.10^{ - 5}}.{x^2} + x\tan \alpha \\ = x.\left[ {\tan \alpha - \left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}.x} \right]\end{array}\)
Khi đó y = 0
Suy ra x = 0 hoặc \(x = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\)
Theo góc bắn \(\alpha \)tầm xa mà quả đạn đạt tới là \(\frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\)
b) Quả đạn trúng mục tiêu cách vị trí đặt khẩu pháp 22 000 m thì x = 22 000 (m)
Khi đó
\(\begin{array}{l}22\,000 = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\\ \Leftrightarrow 0,4312 = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right)}}\\ \Rightarrow \alpha \approx {30^ \circ }\end{array}\)
( Bấm máy tính để tìm giá trị sấp xỉ của \(\alpha \))

Chọn hệ trục Oxy như hình vẽ , chiều dương hướng xuống
Phương trình tọa độ
x = v0.t = 36t (1)
y = \(\dfrac{1}{2}gt^2=5t^2\) (2)
Từ (1) và (2) ta có phương trình quỹ đạo của vật là
(P) : \(y=\dfrac{5}{1296}.x^2\) (*)
Nhận thấy đường thẳng dốc (d) đi qua gốc O nên phương trình
(d) có dạng y = ax
mà \(a=\tan\alpha=\tan30^{\text{o}}=\dfrac{1}{\sqrt{3}}\)
Vậy (d) : \(y=\dfrac{x}{\sqrt{3}}\) (**)
Phương trình hoành độ giao điểm của (d) và (P) :
\(\dfrac{5x^2}{1296}=\dfrac{x}{\sqrt{3}}\) \(\Leftrightarrow x=\dfrac{1296}{5\sqrt{3}}\) (m)
Viên đạn rơi xuống sườn dốc cách dốc khoảng cách
\(x_1=\dfrac{x}{\cos\alpha}=\dfrac{x}{\cos30^{\text{o}}}=172,8\left(m\right)\)