cho hình vẽ biết góc E=110 độ góc B=70 góc C =40 độ. chứng minh DE//BC. tính góc EDC và góc xDC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta thấy:
\(\widehat{BED}+\widehat{EBC}=180^o\)
Mà hai góc này ở vị trí trong cùng phía
\(\Rightarrow DE//BC\)
b) Mà: DE//BC
\(\Rightarrow\widehat{EDC}+\widehat{BCD}=180^o\)(hai góc trong cùng phía)
\(\Rightarrow\widehat{EDC}=180^o-\widehat{BCD}=180^o-40^o=140^o\)
Ta lại có:
\(\widehat{EDC}\) đối đỉnh \(\widehat{xDC}\)
\(\Rightarrow\widehat{xDC}=\widehat{EDC}=140^o\)
a) Ta có:
∠BED + ∠EBC = 110⁰ + 70⁰ = 180⁰
Mà ∠BED và ∠EBC là hai góc trong cùng phía
⇒ DE // BC
b) Do DE // BC
⇒ ∠EDC + ∠DCB = 180⁰ (hai góc trong cùng phía)
⇒ ∠EDC = 180⁰ - ∠DCB
= 180⁰ - 40⁰
= 140⁰
Do DE // BC
⇒ ∠xDC = ∠DCB = 40⁰ (so le trong)

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
Suy ra: DA=DE(hai cạnh tương ứng) và \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(gt)
nên \(\widehat{BED}=90^0\)
hay DE⊥BC
Ta có: DA=DE(cmt)
mà DE<DC(ΔDEC vuông tại E có DC là cạnh huyền)
nên DA<DC
b) Ta có: ΔBAC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)(1)
Ta có: ΔEDC vuông tại E(cmt)
nên \(\widehat{EDC}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}=\widehat{EDC}\)(đpcm)
c) Ta có: BA=BE(gt)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy ra BD là đường trung trực của AE
hay BD\(\perp\)AE(đpcm)
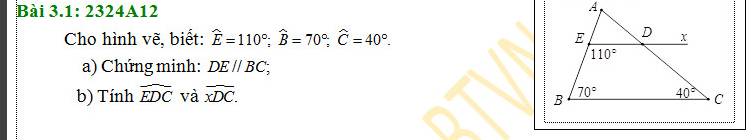
Hình vẽ đâu rồi bạn?