cho hình thang ABCD có AB//CD, M là trung điểm của CD, I là giao điểm của AM và BD, K là giao điểm của BM và AC.a) C/m: IK//ABb) IK cắt AD và BC theo thứ tự tại E và F. C/m: IE=IK=KFc) Gọi O là giao điểm của AC và BD. MO cắt AB tại N, MO cắt BC tại S. CMR: N là trung điểm của AB và 3 điểm A,D,S thẳng hàngnhờ mn giải giúp e...
Đọc tiếp
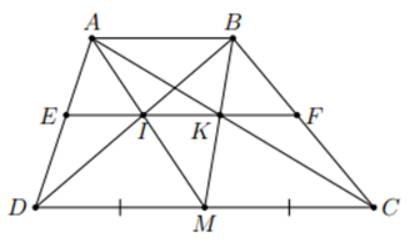
cho hình thang ABCD có AB//CD, M là trung điểm của CD, I là giao điểm của AM và BD, K là giao điểm của BM và AC.
a) C/m: IK//AB
b) IK cắt AD và BC theo thứ tự tại E và F. C/m: IE=IK=KF
c) Gọi O là giao điểm của AC và BD. MO cắt AB tại N, MO cắt BC tại S. CMR: N là trung điểm của AB và 3 điểm A,D,S thẳng hàng
nhờ mn giải giúp e ạ
a: Xét ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=>ΔKAB đồng dạng với ΔKCM
=>KB/KM=AB/CM=AB/MD
Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>IA/IM=AB/MD
=>IA/IM=KB/KM
=>MI/IA=MK/KB
Xét ΔMAB có MI/IA=MK/KB
nên IK//AB
b: Xét ΔADM có EI//DM
nên EI/DM=AI/AM
=>EI/CM=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BK/BM
Xét ΔMAB có IK//AB
nên IK/AB=MK/MB=MI/MA
=>BK/BM=AI/AM
=>EI/DM=KF/DM
=>EI=KF
c: Xét ΔOAN và ΔOCM có
góc OAN=góc OCM
góc AON=góc COM
=>ΔOAN đồng dạng với ΔOCM
=>OA/OC=AN/CM
Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOb=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=AB/CD
=>AB/CD=AN/CM
=>AB/AN=CD/CM=2
=>AB=2AN
=>N là trung điểm của AB