Đáp án D

Hai nguồn giống nhau có thể coi cùng phương trình  u A   =   u B   =   A cos ω t

Phương trình 2 sóng thành phần tại M là 1 điểm bất kì trên đoạn CO

u A M   =   A cos ( ω t   -   2 π λ d 1 ) ,   u B M   =   A cos ( ω t   -   2 π λ d 2 ) . Chú ý ( d 1   =   d 2   =   d )

Phương trình sóng tổng hợp tại M:  u M   =   u A M   +   u B M   =   2 A cos ( ω t   -   2 π λ d )

Để sóng tại M ngược pha với hai nguồn thì  2 π λ d   =   ( 2 k + 1 ) π   ⇒   d   =   ( 2 k + 1 ) λ 2

Do M nằm trên đoạn CO nên d có điều kiện: 6 c m   ≤   d   ≤ 6 2   +   8 2 = 10cm. Hay 3 , 25   ≤   k   ≤ 5 , 75   ⇒ k   =   4 , 5 .

Vậy có 2 điểm thỏa mãn.

Đáp án B

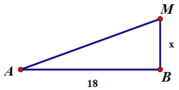
M cực đại nên

M gần B nhất nên k phải max.

Ta có

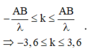
Vì k max nên chọn k = 3. Suy ra MA-MB=15. Lại có

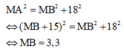
Vậy x = 3,3 thỏa mãn đề bài

\(MA=6cm;MB=AB-MA=20-6=14cm\)

\(AM\perp MC\Rightarrow AC=\sqrt{AM^2+MC^2}=\sqrt{6^2+8^2}=10cm\)

\(BM\perp MC\Rightarrow BC=\sqrt{BM^2+MC^2}=\sqrt{14^2+8^2}=2\sqrt{65}cm\)

Xét một điểm N bất kì trên CM ta có: \(d_2-d_1=k\lambda\)

Hai nguồn dao động cùng pha:

\(\Rightarrow\left\{{}\begin{matrix}d_2-d_1=\left(k+0,5\right)\lambda\\BC-AC\le k\lambda\le BM-AM\end{matrix}\right.\)

\(\Rightarrow2\sqrt{65}-10\le k+0,5\le14-6\Rightarrow5,62\le k\le7,5\)

\(\Rightarrow k=\left\{6,5;7,5\right\}\)

Vậy có hai điểm cực tiểu trên CD.

Chọn đáp án D.

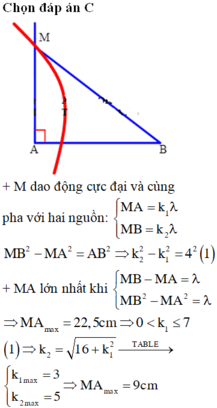
- Giả sử: MA = k. λ = 4k

Và MB = m. λ  = 4m

+ Ta có:  M A 2 + M B 2 ≤ A B 2

=> k 2 + m 2 ≤ 121 4

+ M ở xa A nhất khi và chỉ khi  K m a x  có thể a luôn có: MA ≤  AB = 22

=> 4K  ≤  22

=>  K m a x  = 5

- Điểm M cách xa A nhất một đoạn bằng: 5 λ  = 20 cm thì ta cần có:

25 + m²  ≤   121 4

=> m ≤ 2,2

=> m = 1 hoặc m = 2

- Với m = 1 ta có: MA - MB = 4 λ , tức là điểm M nằm trên cực đại số 4 cách A khoảng 20 cm và B là 4 cm

- Tương tự với m = 2 thì ta có:

+ Do mỗi đường cục đại này cho 2 điểm đối xứng nhau qua AB

=> Nên tổng là 4 điểm

Đáp án A

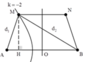
Số điểm dao động với biên độ cực đại trên AB

- A B λ ≤ k ≤ A B λ ⇔ - 8 ≤ k ≤ 8

Để diện tích AMNB là lớn nhất thì M phải nằm trên cực đại ứng với k=-2

d 1 - d 2 = - 2 k λ = - 2     c m .

Mặc khác  d 1 2 = A H 2 + M H 2 d 2 2 = B H 2 + M H 2 ⇒ d 1 + d 2 = B H 2 - A H 2 2 = 16     c m

Ta tính được  d 1 = 7     c m  từ đó suy ra   M H = 2 5     c m .

Diện tích hình thang  S A M N B = 1 2 A B + M N M H = 18 5     c m 2 .