Cho hình chóp S.abcd,có đáy ABCD là hình bình hành. Lấy M là trung điểm của SA, N thuộc SD sao cho SN=2SD a)tìm giao điểm của MN và (ABCD) b) tìm giao điểm của CM và (SBD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Chọn mp(SAB) có chứa MN
Ta có: \(AB\subset\left(SAB\right)\)
\(AB\subset\left(ABCD\right)\)
Do đó: \(\left(SAB\right)\cap\left(ABCD\right)=AB\)
Gọi P là giao điểm của MN với AB
=>P là giao điểm của MN với mp(ABCD)
b: Ta có: SN+NB=SB
=>2NB+NB=SB
=>SB=3NB
=>\(\dfrac{SN}{SB}=\dfrac{2}{3}\)
Xét ΔSBA có P,M,N thẳng hàng
nên \(\dfrac{PB}{PA}\cdot\dfrac{MA}{MS}\cdot\dfrac{NS}{NB}=1\)
=>\(\dfrac{PB}{PA}\cdot1\cdot2=1\)
=>\(\dfrac{PB}{PA}=\dfrac{1}{2}\)
=>B là trung điểm của AP
Trong mp(ABCD), gọi O là giao điểm của AC và BD
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAPC có
B,O lần lượt là trung điểm của AP,AC
=>BO là đường trung bình của ΔAPC
=>BO//PC
=>BD//PC
Ta có: PC//BD
BD\(\subset\)(SBD)
PC không nằm trong mp(SBD)
Do đó: PC//(SBD)

Gọi giao của AC và BD là O
\(\left\{{}\begin{matrix}O\in AC\subset\left(SAC\right)\\O\in BD\subset\left(SBD\right)\end{matrix}\right.\Leftrightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\Leftrightarrow S\in\left(SAC\right)\cap\left(SBD\right)\)
=>(SAC) giao (SBD)=SO

Đáp án D
Gọi O = A C ∩ B D ⇒ V S . A B C D = a 3 3 ,
Vì O M / / S D ⇒ N D / / O M ⇒ N D / / M A C
Vì d N , A M C = d D , A M C = d B , A M C ⇒ V N . A M C = V D . M A C = V B . M A C = 1 4 V S . A B C D = a 3 12

a: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình
=>MN//BD
BD//MN
\(MN\subset\left(AMN\right)\)
BD không thuộc mp(AMN)
Do đó: BD//(AMN)
b: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Chọn mp(SBD) có chứa MN
(SBD) giao (SAC)=SO(cmt)
Gọi K là giao điểm của SO với MN
=>K là giao điểm của MN với mp(SAC)
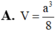
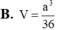
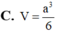
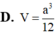
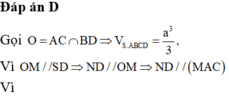
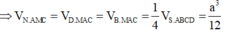
a: Trong mp(SAD), gọi E là giao điểm của MN với AD
\(E\in MN\)
\(E\in AD\subset\left(ABCD\right)\)
Do đó: \(E=MN\cap\left(ABCD\right)\)
b: Chọn mp(SAC) có chứa CM
Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(SO=\left(SAC\right)\cap\left(SBD\right)\)
Gọi K là giao của SO và CM
=>K là giao điểm của CM với (SBD)