Cho góc xOy và tia Oz nằm giữa hai tia Ox và Oy. Từ điểm A trên tia Oz vẽ AH\(⊥\)Ox, AK \(⊥\)Oy. Gọi E, F lần lượt là hình chiếu của H và K trên Oz, gọi B là giao điểm của HK và Oz. Chứng minh rằng: \(\frac{EA.EO}{FA.FO}\)= \(\frac{BH^2}{BK^2}\).MÌNH ĐANG CẦN GẤP, CẢM ƠN CÁC BẠN NHIỀU :P
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

13 tháng 7 2017
Có \(\Delta HEB~\Delta KFB\left(g-g\right)\)=> \(\frac{HE}{KF}=\frac{BH}{BK}\)=> \(\frac{HE^2}{KF^2}=\frac{BH^2}{BK^2}\)(1)
Có \(HE^2=EA.EO\)(TỰ XÉT TAM GIÁC NHA) (2)
\(KF^2=FA.FO\)(3)
tỪ (1),(2),(3) => \(\frac{EA.EO}{FA.FO}=\frac{BH^2}{BK^2}\)(đpcm)

21 tháng 12 2021
a: Xét tứ giác BOAE có
I là trung điểm của BA
I là trung điểm của OE
Do đó: BOAE là hình bình hành
Suy ra: BE//OA

HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
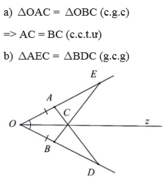
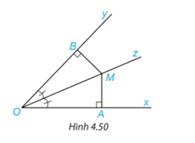
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)