a: góc IBC=góc ABC/2

góc ICB=góc ACB/2

mà góc ABC=góc ACB

nên góc IBC=góc ICB

=>ΔIBC cân tại I

b: AB=AC

IB=IC

=>AI là trung trực của BC

a, Ta có: Tam giác ABC cân tại A (gt)

=> góc ABC = góc ACB

=> 1/2 góc ABC = 1/2 góc ACB

=> góc IBC = góc ICB

=> Tam giác BIC cân tại I

b, Gọi M là giao điểm của AI với BC

Ta có tam giác BIC cân (câu a)

=> IB = IC ( cặp góc tương ứng )

Xét tam giác ABI và tam giác ACI:

AB = AC (gt)

góc ABI = góc ACI (c.m trên )

IB = IC (c.m trên )

=> Tam giác ABI = tam giác ACI (c.g.c)

=>góc BAI = góc CAI ( cặp góc tương ứng )

Xét tam giác BAM và tam giác CAM

góc BAI = góc CAI (c.m trên)

AB = AC (gt)

góc ABC = góc ACB (gt)

=> tam giác BAM = tam giác CAM (g.c.g)

=>BM = CM (cặp cạnh tương ứng) (1)

=>góc AMB = góc AMC (cặp góc tương ứng )

mà góc AMB + góc AMC = 180^o (kề bù)

=> góc AMB = góc AMC = 180^o / 2 = 90^o (2)

Từ (1)(2) => AI trung trực BC

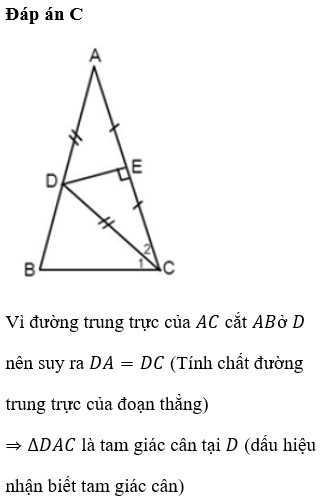
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAD}\) chung

Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)

b) Xét ΔBEC vuông tại E và ΔCDB vuông tại D có 

BC chung

\(\widehat{EBC}=\widehat{DCB}\)(hai góc ở đáy của ΔABC cân tại A)

Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)

Suy ra: \(\widehat{BCE}=\widehat{DBC}\)(hai góc tương ứng)

hay \(\widehat{IBC}=\widehat{ICB}\)

Xét ΔIBC có \(\widehat{IBC}=\widehat{ICB}\)(cmt)

nên ΔIBC cân tại I(Định lí đảo của tam giác cân)

\(\Leftrightarrow IB=IC\)(hai cạnh bên)

Xét ΔBAI và ΔCAI có 

BA=CA(ΔABC cân tại A)

AI chung

IB=IC(cmt)

Do đó: ΔBAI=ΔCAI(c-c-c)

Suy ra: \(\widehat{BAI}=\widehat{CAI}\)(hai góc tương ứng)

c) Ta có: AB=AC(ΔABC cân tại A)

nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: IB=IC(cmt)

nên I nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)

Từ (1) và (2) suy AI là đường trung trực của BC(đpcm)

https://hoc24.vn/cau-hoi/cho-tam-giac-abc-can-tai-a-ke-bd-vuong-goc-voi-ac-va-ke-ce-vuong-goc-voi-ab-bd-va-ce-cat-nhau-tai-i-chung-minh-goc-bai-goc-cai-ai-la-trung-truc.69327720128

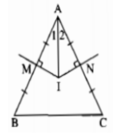
Gọi M, N là trung điểm của AB và AC.

Ta có: AM = 1/2 AB (gt); AN = 1/2 AC (gt)

Mà AB = AC (gt)

⇒ AM = AN

Xét hai tam giác vuông AMI và ANI, ta có:

∠(AMI) = ∠(ANI) = 90o

AM = AN (chứng minh trên)

AI cạnh huyền chung

⇒ ΔAMI= ΔANI (cạnh huyền, cạnh góc vuông)

⇒ ∠(A1) = ∠(A2) (hai góc tương ứng)

Vậy AI là tia phân giác của ∠(BAC)

+Tham Khảo

Giống nhau :v ghê 

Gọi M, N là trung điểm của AB, AC

Xét hai tam giác vuông AMI và ANI có:

AI: cạnh huyền chung

AM = AN (gt)

Vậy: \(\Delta AMI=\Delta ANI\left(ch-cgv\right)\)

Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)

Do đó: AI là tia phân giác của góc A.