Cho tam giác ABC vuông ở A, đường cao AH. Chứng minh rằng:
a) Tam giác ABC đồng dạng với tam giác HBA;
b) AB BH.BC 2 ;
c) AH BH.HC 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: \(\dfrac{S_{ABC}}{S_{HBA}}=\dfrac{25}{9}\)
nên \(S_{HBA}=24:\dfrac{25}{9}=24\cdot\dfrac{9}{25}=8.64\left(cm^2\right)\)

Mình đã giải xong câu a, b, c. Nhờ các bạn và quý thầy cô giải giúp câu d. Chỉ cần tóm tắt lời giải thôi cũng được ạ.
d) SADE = 1/2.AD.AE ; SABC = 1/2.AB.AC => SADE / SABC = AD.AE/AB.AC =1/4 (1)
Do tg ADE đồng dạng tg ABC => SADE / SABC = (DE/BC)2 = (AH/BC)2 (2)
Từ (1) và (2) => AH/BC = 1/2 hay AH = !/2 BC. Vậy AH là đường trung tuyến tg ABC, mà AH là đường cao => tg ABC cân tại A

a.Xét tam giác HBA và tam giác ABC, có:
^AHB = ^CAB = 90 độ
^B: chung
Vậy tam giác HBA đồng dạng tam giác ABC ( g.g )
b.
Áp dụng định lý pitago, ta có:
\(BC=\sqrt{8^2+10^2}=2\sqrt{41}cm\)
Ta có: tam giác HBA đồng dạng tam giác ABC
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\)
\(\Leftrightarrow\dfrac{AH}{10}=\dfrac{8}{2\sqrt{41}}\)
\(\Leftrightarrow AH=\dfrac{8.10}{2\sqrt{41}}=\dfrac{40\sqrt{41}}{41}cm\)
Ta có: tam giác HBA đồng dạng tam giác ABC
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{AB}{BC}\)
\(\Leftrightarrow AB^2=HB.BC\)
\(\Leftrightarrow8^2=2\sqrt{41}HB\)
\(\Leftrightarrow HB=\dfrac{32\sqrt{41}}{41}cm\)

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
b: ΔBAC đồng dạng vơi ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
c: ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AD/DC=BA/BC=6/10=3/5
b: Xét ΔHBA vuông tạiH và ΔABC vuôg tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
màgóc DBC=góc ABD
nên góc AID=góc ADI
=>ΔAID cân tại A

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB^2=6^2-4,8^2=3,6^2\)
=>HB=3,6(cm)
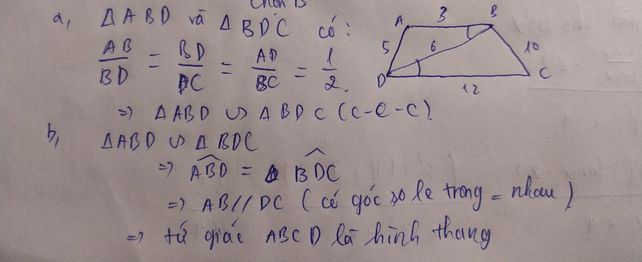 lời giải đây nhé e ❤️. tham khảo nhé!
lời giải đây nhé e ❤️. tham khảo nhé!
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔBAC đồng dạng với ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
c: Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
góc HAC=góc HBA
=>ΔHAC đồng dạng với ΔHBA
=>HA/HB=HC/HA
=>HA^2=HB*HC
em cảm ơn anh rất nhiều ạ