Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hướng dẫn, ghét hình học phẳng:
Để ý rằng AB vuông góc (M) tại H nên AH, BH cũng là các tiếp tuyến của (M)
- Nối MA, MB
- \(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn (O) nên suy ra...
- AH, AC là 2 tiếp tuyến \(\Rightarrow\widehat{AMC}=\widehat{AMH}\)
Tương tự: \(\widehat{BMD}=\widehat{BMH}\)
\(\Rightarrow\widehat{CMD}=2\left(\widehat{AMH}+\widehat{BMH}\right)\)
b. AC, AH, BD, BH là các tiếp tuyến nên \(\left\{{}\begin{matrix}AC=AH\\BD=BH\end{matrix}\right.\) \(\Rightarrow AC+BD=...\)
c.
AC song song BD (cùng vuông CD), O và M lần lượt là trung điểm AB, CD
\(\Rightarrow OM\) là đtb hình thang vuông ABDC \(\Rightarrow OM\) vuông CD
Hệ thức lượng tam giác vuông OMK: \(OM^2=OH.OK\)
Mà \(OM=\dfrac{AB}{2}\Rightarrow...\)
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm
a: Xét hình thang AHKB có
O là trung điểm của AB
OM//AHKB
Do đó: M là trung điểm của HK
b: Kẻ MN vuông góc với AB
Xét tứ giác AHMN có \(\widehat{AHM}+\widehat{ANM}=180^0\)
=>AHMN là tứ giác nội tiếp
=>\(\widehat{MAN}=\widehat{MHN}\)
Xét tứ giác MNBK có \(\widehat{MNB}+\widehat{MKB}=180^0\)
=>MNBK nội tiếp
=>\(\widehat{MBN}=\widehat{MKN}\)
Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{NHK}+\widehat{NKH}=90^0\)
=>ΔNKH vuông tại N
ΔNKH vuông tại N có NM là trung tuyến
nên MH=MN
Xét (M) có
MN là bán kính
AB vuông góc MN tại N
Do đó: AB là tiếp tuyến của (M)
=>ĐPCM
b) Gọi I là tâm của đường tròn đường kính CD.
Tứ giác CABD là hình thang vuông (AC ⊥ AB;BD ⊥ AB) có OI là đường trung bình
⇒ OI // AC ; mà AC ⊥ AB ⇒ OI ⊥ AB tại O
Vậy AB tiếp xúc với đường tròn đường kính CD.
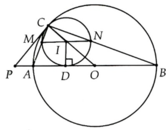
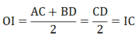
a) Ta thấy do AC, AH là tiếp tuyến qua A của đường tròn tâm M nên theo tính chất hai tiếp tuyến cắt nhau suy ra \(\widehat{CMA}=\widehat{AMH}\)
Tương tự \(\widehat{DMB}=\widehat{HMB}\)
Mà do M thuộc đường tròn tâm O nên \(\widehat{AMB}=90^o\Rightarrow\widehat{AMH}+\widehat{HMB}=90^o\)
\(\Rightarrow\widehat{CMD}=2.90^o=180^o\) hay C, M, D thẳng hàng.
Khi đó ACDB là hình thang, có OA = OB, MC = MD nên OM là đường trung bình. Vậy OM// DB hay OM vuông góc với CD tại M.
Nói các khác, M, C, D thuộc tiếp tuyến của (O) tại M.
b) Ta thấy theo tính chất hai tiếp tuyến cắt nhau thì AC = AH, BD = BH nên AC + BD = AH + HB = AB = 2R (không đổi)
Ta thấy CD = 2MH
Xét tam giác vuông AMB, theo hệ thức lượng ta có: AH.HB = MH2
Vậy nên \(AC.BD=\left(\frac{CD}{2}\right)^2=\frac{CD^2}{4}\)
c) Xét tam giác KMO vuông tại M, áp dụng hệ thức lượng ta có: OH.OK = MO2
Mà OM = OA = OB nên OH.OK = OA2 = OB2.