x3 + 2x2y +xy2 - 25x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: =(2x+y-2y)(2x+y+2y)
=(2x-y)(2x+3y)
2: =(4-5x)(16+20x+25x^2)
3: =x(x^2-2xy+y^2-4)
=x[(x-y)^2-4]
=x(x-y-2)(x-y+2)
4: =(x-y)(x^2+xy+y^2)+xy(x-y)
=(x-y)(x^2+2xy+y^2)
=(x-y)(x+y)^2
1: =(2x+y-2y)(2x+y+2y)
=(2x-y)(2x+3y)
2: =(4-5x)(16+20x+25x^2)
3: =x(x^2-2xy+y^2-4)
=x[(x-y)^2-4]
=x(x-y-2)(x-y+2)
4: =(x-y)(x^2+xy+y^2)+xy(x-y)
=(x-y)(x^2+2xy+y^2)
=(x-y)(x+y)^2

\(x^3+2x^2y+xy^2-9x\)
\(=x\left(x^2+2xy+y^2-9\right)\)
\(=x\left[\left(x^2+2xy+y^2\right)-9\right]\)
\(=x\left[\left(x+y\right)^2-9\right]\)
\(=x\left(x+y+3\right)\left(x+y-3\right)\)
Bài 2 : Cho hình thang ABCD (AB // CD). Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự tại E và F. Chứng minh: 𝐴𝐸/𝐴𝐷 + 𝐶𝐹/𝐵𝐶 = 1


x3 + 2x2y + xy2 – 9x
(Có x là nhân tử chung)
= x(x2 + 2xy + y2 – 9)
(Có x2 + 2xy + y2 là hằng đẳng thức)
= x[(x2 + 2xy + y2) – 9]
= x[(x + y)2 – 32]
(Xuất hiện hằng đẳng thức (3)]
= x(x + y – 3)(x + y + 3)

a) x3 + 2x2y + xy2 – 4x = x(x2 + 2xy + y2– 4) = x[(x+y)2-4]
= x(x + y + 2)(x + y – 2)

a: \(=x^2\left(2x+3\right)+\left(2x+3\right)\)
\(=\left(2x+3\right)\left(x^2+1\right)\)
b: \(=\left(x-4\right)\left(x+3\right)\)
e: =(x+3)(x-2)
a) \(=x^2\left(2x+3\right)+\left(2x+3\right)=\left(2x+3\right)\left(x^2+1\right)\)
b) \(=x\left(x-4\right)+3\left(x-4\right)=\left(x-4\right)\left(x+3\right)\)
c) \(=\left(2x\right)^2-\left(x^2+1\right)^2=\left(x^2-2x+1\right)\left(x^2+2x+1\right)=\left(x-1\right)^2\left(x+1\right)^2\)
d) \(=4xy\left(y-3x+2\right)\)
e) \(=x\left(x-2\right)+3\left(x-2\right)=\left(x-2\right)\left(x+3\right)\)
f) \(=x\left(x^2+2xy+y^2-4z^2\right)=x\left[\left(x+y\right)^2-4z^2\right]=x\left(x+y-2z\right)\left(x+y+2z\right)\)
g) \(=x\left(x^2-2xy+y^2-25\right)=x\left[\left(x-y\right)^2-25\right]=x\left(x-y-5\right)\left(x-y+5\right)\)
h) \(=x\left(x+1\right)-3\left(x+1\right)=\left(x+1\right)\left(x-3\right)\)
i) \(=x^2\left(x-3\right)-9\left(x-3\right)=\left(x-3\right)\left(x^2-9\right)=\left(x-3\right)^2\left(x+3\right)\)
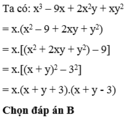
\(x^3+2x^2y+xy^2-25x\)
\(=x\left(x^2+2xy+y^2-25\right)\)
\(=x\left[\left(x+y\right)^2-5^2\right]\)
\(=x\left(x+y-5\right)\left(x+y+5\right)\)
= ( x3 + 2x2y + xy2 ) - 25x
= x.(x2 + 2xy + y2 ) - 5x2
= x.( x + y )2 - 5x2
= x. [(x + y) + 5x]. [( x + y) - 5x]