Ta có: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=4\left(a^2+b^2+c^2-ab-ac-bc\right)\)

\(\Leftrightarrow a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ac+a^2=4a^2+4b^2+4c^2-4ab-4bc-4ac\)

\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=4a^2+4b^2+4c^2-4ab-4ac-4bc\)

\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac-4a^2-4b^2-4c^2+4ab+4bc+4ac=0\)

\(\Leftrightarrow-2a^2-2b^2-2c^2+2ab+2ac+2bc=0\)

\(\Leftrightarrow-\left(2a^2+2b^2+2c^2-2ab-2bc-2ac\right)=0\)

\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)

\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\Leftrightarrow a=b=c\)(đpcm)

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=4\left(a^2+b^2+c^2-ab-ac-bc\right)\)

\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc=4\left(a^2+b^2+c^2-ab-ac-bc\right)\)

\(\Leftrightarrow2\left(a^2+b^2+c^2-ab-ac-bc\right)=4\left(a^2+b^2+c^2-ab-ac-bc\right)\)

\(\Leftrightarrow2\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)

\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)

\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)

Vì \(\hept{\begin{cases}\left(a-b\right)^2\ge0\\\left(b-c\right)^2\ge0\\\left(c-a\right)^2\ge0\end{cases}\forall a;b;c}\)

\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)

Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\\\left(c-a\right)^2=0\end{cases}\Rightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}\Rightarrow}\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Rightarrow}a=b=c}\)

Vậy \(a=b=c\)

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=4\left(a^2+b^2+c^2-ab-ac-bc\right)\)

<=>\(a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=4a^2+4b^2+4c^2-4ab-4ac-4bc\)

<=>\(2a^2+2b^2+2c^2-2ab-2bc-2ca\)\(=4a^2+4b^2+4c^2-4ab-4ac-4bc\)

<=>\(0=2a^2+2b^2+2c^2-2ab-2bc-2ca\)

<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)

<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)

Vì \(\hept{\begin{cases}\left(a-b\right)^2\ge0\\\left(b-c\right)^2\ge0\\\left(c-a\right)^2\ge0\end{cases}}\)=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)

Dấu "=" xảy ra khi \(\left(a-b\right)^2=\left(b-c\right)^2=\left(c-a\right)^2=0\)<=> a-b=b-c=c-a <=> a=b=c

vế phải= \(2\left(2a^2+2b^2+2c^2-2ab-2bc-2ac\right)\)

=\(2\left[\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)\right]\)

=\(2\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\)

=>\(\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]-2\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\)

\(\Leftrightarrow-1\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\)

\(\Leftrightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}}\Leftrightarrow a=b=c\)

(

hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh

hhhhhhhhhhhhhhhhh

hhhhhhhhhhhhhhhhhh

hhhhhhhhhhhhhhh

hhhhhhhhhhhhh

Dễ dàng c/m : \(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}=1\)

Ta có : \(\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le\dfrac{1}{a+b+4}\le\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}\right)\) 

Suy ra : \(\Sigma\dfrac{1}{\sqrt{2\left(a^2+b^2\right)}+4}\le2.\dfrac{1}{4}\left(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}\right)=\dfrac{1}{2}.1=\dfrac{1}{2}\) 

" = " \(\Leftrightarrow a=b=c=1\)

 Dạ em cám ơn nhiều lắm ạ

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=4\left(a^2+b^2+c^2-ab-ac-bc\right)\\ \Leftrightarrow a^2-2ab+b^2+b^2-2bc-c^2+c^2-2ac+a^2\\ =4a^2+4b^2+4c^2-4ab-4ac-4bc\\ \Leftrightarrow0=2a^2+2b^2+2c^2-2ab-2ac-2bc\\ \Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2ac+c^2\right)+\left(b^2-2bc+c^2\right)=0\\ \Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2=0\Leftrightarrow\left\{\begin{matrix}\left(a-b\right)^2=0\Leftrightarrow a-b=0\Leftrightarrow a=b\\\left(a-c\right)^2=0\Leftrightarrow a-c=0\Leftrightarrow a=c\\\left(b-c\right)^2=0\Leftrightarrow b-c=0\Leftrightarrow b=c\end{matrix}\right.\)

Vậy a=b=c

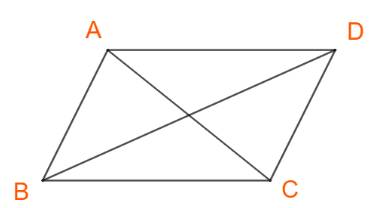
a) Áp dụng định lí cosin ta có:

\(\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos ABC\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\end{array} \right.\)

Mà \(AD = BC;\cos BAD = \cos ({180^ \circ } - ABC) =  - \cos ABC\) 

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos BAD\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos BAD\end{array} \right.\end{array}\)

Cộng vế với vế ta được:

\( A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\)

b)  Theo câu a, ta suy ra: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\)

\(\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}\)