Bài 1:Cho góc nhọn xOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Trên tia Ax lấy điểm C,trên tia By lấy điểm D sao cho AC=BDa) Chứng minh:AD=BCb) Gọi E là giao điểm AD và Bc.Chứng minh:\(\Delta EAC=\Delta EBD\)c) Chứng minh:OE là phân giác của góc xOyBài 2:Cho \(\Delta ABC\)có \(\widehat{A}=90^o\).Kẻ AH vuông góc với BC \(\left(H\varepsilon BC\right)\).Trên đường thẳng vuông góc với BC tại B lấy điểm D...
Đọc tiếp
Bài 1:
Cho góc nhọn xOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Trên tia Ax lấy điểm C,trên tia By lấy điểm D sao cho AC=BD
a) Chứng minh:AD=BC
b) Gọi E là giao điểm AD và Bc.Chứng minh:\(\Delta EAC=\Delta EBD\)
c) Chứng minh:OE là phân giác của góc xOy
Bài 2:
Cho \(\Delta ABC\)có \(\widehat{A}=90^o\).Kẻ AH vuông góc với BC \(\left(H\varepsilon BC\right)\).Trên đường thẳng vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho BD=AH
Chứng minh rằng:
a) \(\Delta AHB=\Delta DBH\)
b) AB//DH
c) Tính \(\widehat{ACB}\),biết \(\widehat{BAH=35^o}\)
Bài 3:
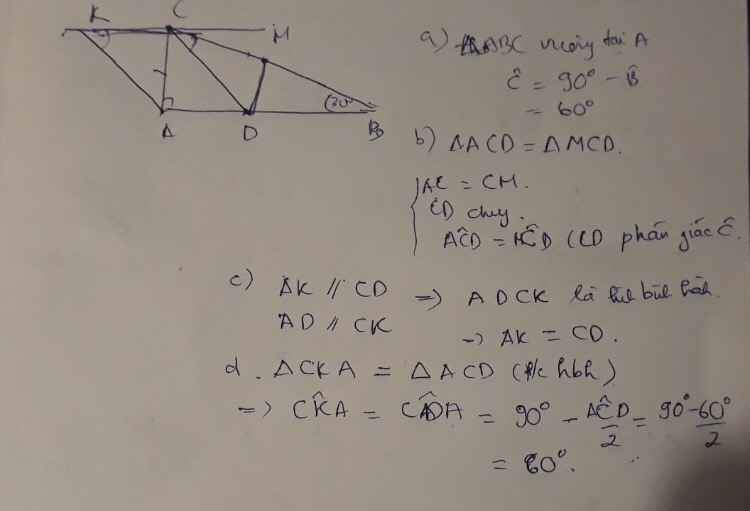
Cho \(\overline{\Delta}ABC\) vuông tại A có \(\overline{\Delta}B=30^o\)
a) Tính \(\Delta C\)
b) Vẽ tia phân giác của góc C cắt cạnh AB tại D
c) Trên cạnh CB lấy điểm M sao cho CM=CA.Chứng minh \(\Delta ACD=\Delta MCD\)
d) Qua C vẽ đường thẳng xy vuông góc CA.Từ A kẻ đường thẳng song song với CD cắt xy ở K.Chứng minh:AK=CD
e) Tính \(\DeltaẠKC\)
Bài 4:
Cho tam giác ABC vuông tại A,có AB=AC.Gọi K là trung điểm của cạnh BC
a) Chứng minh \(\Delta AKB=\Delta AKC\)và \(AK⊥BC\)
b) Từ C kẻ đường vuông góc với BC,nó cắt AB tại E.Chứng minh EC//AK
c) Chứng minh CE=CB

mk viết ngắn gọn thui nhé:
a) góc C = 1800 - Â - B = 1800 - 900 - 300 = 600
b) * tam giác ACD = tam giác MCD (c.g.c) . Vì:
CD : cạnh chung
góc ACD = góc MCD
AC = MC
* Xét 2 tam giác vuông: ACK và CDA:
góc ACD = góc CAK (2 góc so le trong)
AC : cạnh chung
=> tam giác ACK = tam giác CDA (cạnh góc vuông - góc nhọn kề)
=> AK = CD (2 cạnh tương ứng)
c) theo câu b: tam giác ACK = tam giác CDA (cạnh góc vuông - góc nhọn kề)
=> góc AKC = góc ADC (2 góc tương ứng)
Trong tam giác ACD, có:
góc ADC = 1800 - góc A - (góc ACB : 2) = 1800 - 900 - 600 : 2 = 600
=> góc AKC = góc ADC = 600