Bài 5 là rút gọn biểu thức ạ, mng giúp tớ vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x-\left(\dfrac{1}{2}sin4x-\dfrac{1}{2}sin2x\right)\)
\(=\dfrac{1}{2}sin6x-\dfrac{1}{2}sin4x\)
\(=cos5x.sinx\)

a: \(B=\left(\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x-2}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(=\dfrac{x-2x-4+x-2}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2-4+10-x^2}{x+2}\)
\(=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{6}=\dfrac{-1}{x-2}\)
b: Khi x=1/2 thì \(B=\dfrac{-1}{\dfrac{1}{2}-2}=\dfrac{2}{3}\)
Khi x=-1/2 thì B=2/5
c: Để B nguyên thì \(x-2\in\left\{1;-1\right\}\)
hay \(x\in\left\{3;1\right\}\)
a, đk : x khác -2 ; 2
\(B=\left(\dfrac{x-2\left(x+2\right)+x-2}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{x^2-4+10-x^2}{x+2}\right)\)
\(=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}:\dfrac{6}{x+2}=\dfrac{1}{2-x}\)
b, Ta có \(\left|x\right|=\dfrac{1}{2}\Leftrightarrow x=\dfrac{1}{2};x=-\dfrac{1}{2}\)
Với x = 1/2 ta được \(B=\dfrac{1}{2-\dfrac{1}{2}}=\dfrac{2}{3}\)
Với x = -1/2 ta được \(B=\dfrac{1}{2+\dfrac{1}{2}}=\dfrac{2}{5}\)
c, \(\dfrac{1}{2-x}\Rightarrow2-x\inƯ\left(1\right)=\left\{\pm1\right\}\)
| 2-x | 1 | -1 |
| x | 1 | 3 |

a: Ta có: \(P=\left(\dfrac{1}{a+\sqrt{a}}+\dfrac{1}{\sqrt{a}+1}\right):\dfrac{\sqrt{a}-1}{a+2\sqrt{a}+1}\)
\(=\dfrac{a+1}{\sqrt{a}\left(\sqrt{a}+1\right)}\cdot\dfrac{\left(\sqrt{a}+1\right)^2}{\sqrt{a}-1}\)
\(=\dfrac{\left(a+1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}\)

d: \(\dfrac{-\left(\sqrt{3}-\sqrt{6}\right)}{1-\sqrt{2}}+\dfrac{6\sqrt{3}+3}{\sqrt{3}}-\dfrac{13}{4+\sqrt{3}}\)
\(=-\sqrt{3}+6+\sqrt{3}-4+\sqrt{3}\)
\(=2+\sqrt{3}\)

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề hơn.

CN : tôi
VN : còn lại
TN : Mãi đến năm nay , khi đã lên lớp 5

\(M=\left(\dfrac{\sqrt{x}}{2x}-\dfrac{1}{\sqrt{x}}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\\ =\left(\dfrac{\sqrt{x}}{2x}-\dfrac{2\sqrt{x}}{2x}\right)\cdot\left(\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x-2\sqrt{x}}{2x}\cdot\dfrac{x-2\sqrt{x}+1-\left(x+2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-2\right)}{x-1}\)

Đề bài ko chính xác, nếu x bất kì thì tồn tại vô số x để P nguyên
Nếu \(x\) nguyên thì mới có hữu hạn giá trị x

a: Ta có: \(\left(x+y\right)^2+\left(x-y\right)^2-2x^2\)
\(=x^2+2xy+y^2+x^2-2xy+y^2-2x^2\)
\(=2y^2\)
b: Ta có: \(\left(x+1\right)^3-\left(x-1\right)\left(x^2+x+1\right)-3x\left(x+1\right)\)
\(=x^3+3x^2+3x+1-x^3+1-3x^2-3x\)
=2
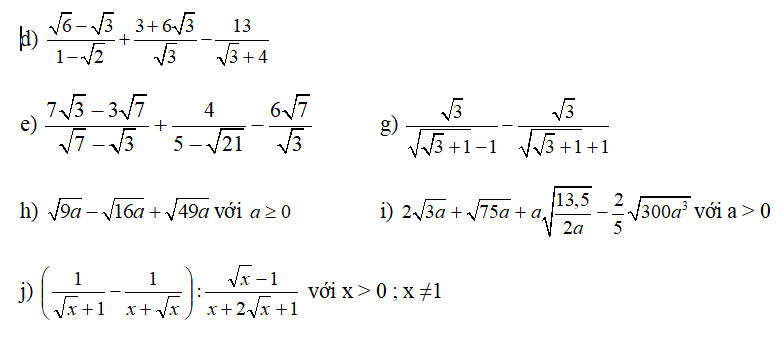
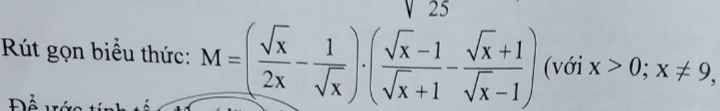
13.
$(x+4)^2+(x+5)(x-5)-2x(x+1)$
$=(x^2+8x+16)+(x^2-25)-(2x^2+2x)$
$=x^2+8x+16+x^2-25-2x^2-2x$
$=(x^2+x^2-2x^2)+(8x-2x)+(16-25)=6x-9$
14.
$(x-1)^2-2(x+3)(x-3)+4x(x-4)$
$=(x^2-2x+1)-2(x^2-9)+(4x^2-16x)$
$=x^2-2x+1-2x^2+18+4x^2-16x$
$=(x^2-2x^2+4x^2)+(-2x-16x)+(1+18)=3x^2-18x+19$
15.
$(y-3)(y+3)(y^2+9)-(y^2+2)(y^2-2)$
$=(y^2-9)(y^2+9)-(y^4-4)$
$=(y^4-81)-(y^4-4)=-81+4=-77$