cho nửa đường tròn tâm o bán kính AB kẻ tiếp tuyến Ax,By với nửa đg tròn lấy điểm c bất kì trên nửa đường tròn qa c kẻ tiếp tuyến với nửa đường tròn nó cắt Ax tại D , By tại e
tính góc DOE
CMR DE=AD+BE
khi C di chuyển trên nửa đường tròn thì tích CD và CE không đổi
CMR AB là tiếp tuyến của đường tròn ,đường kính BF
Gọi M là giao điểm của AC và BO N là giao điểm của BC và OE cmr MN không đổi khi C di chuyển trên nửa đường tròn
KHI điểm M ở đâu trên nửa đường tròn thì độ dài DE nhỏ nhất
AI GIÚP MIK LÀM BÀI NÀY VỚI !!!

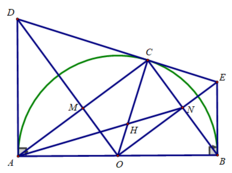
a: Xét (O) có
DC,DA là tiếp tuyến
=>DC=DA và OD là phân giác của góc AOC(1)
Xét (O) có
EC,EB là tiếp tuyến
=>EC=EB và OE là phân giác của góc BOC(2)
Từ (1), (2) suy ra:
góc DOE=1/2(góc COA+góc COB)
=1/2*180=90 độ
b: DC+CE=DE
DC=DA
EB=EC
Do đó: DA+EB=DE
c: Xét ΔDOE vuông tại O có OC là đường cao
nên CD*CE=CO^2
=>CD*CE=R^2 không đổi
d: Sửa đề; Đường kính DE
Gọi K là trung điểm của DE
ΔDOE vuông tại O
=>O nằm trên đường tròn đường kính DE
=>O nằm trên (K)
Xét hình thang ADEB có
K,O lần lượt là trung điểm của DE,AB
=>KO là đường trung bình
=>KO//AD//EB
=>KO vuông góc AB
Xét (K) có
KO là bán kính
AB vuông góc KO tại O
Do đó: AB là tiếp tuyến của (K)