cậu viết câu hỏi ra ik

Công thức tính lực đẩy Achimedes:

F_A = d . V

Trong đó:

F_A là Lực đẩy Achimedes (đơn vị N)

d là khối lượng riêng của chất lỏng (đơn vị N/m³)

V là thể tích phần chất lỏng bị chiếm chỗ (đơn vị m³)

coi bộ dài à nha bn

CHÚC BN THI TỐT NHA!

Câu 17:

Để (d) là hàm số bậc nhất thì \(\left\{{}\begin{matrix}a^2-4=0\\2a-4b\ne0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a^2=4\\a-2b\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\in\left\{2;-2\right\}\\b\ne\dfrac{a}{2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a\in\left\{2;-2\right\}\\b\notin\left\{1;-1\right\}\end{matrix}\right.\)

Câu 16:

a: Ta có: ΔOCI vuông tại C

=>\(OC^2+CI^2=OI^2\)

=>\(OC^2=6^2-\left(3\sqrt{3}\right)^2=9\)

=>\(OC=\sqrt{9}=3\left(cm\right)\)

b:

Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó: ΔBAC vuông tại A

Ta có: BA\(\perp\)AC

OK//BA

Do đó: OK\(\perp\)AC

Ta có: ΔOAC cân tại O

mà OI là đường cao

nên OI là phân giác của góc AOC

Xét ΔOCI và ΔOAI có

OC=OA

\(\widehat{COI}=\widehat{AOI}\)

OI chung

Do đó: ΔOCI=ΔOAI

=>\(\widehat{OCI}=\widehat{OAI}=90^0\)

=>IA là tiếp tuyến của (O)

lm hết à e

1 The distance  from my home to  school is about 3 km

2 My mum used to live in a small village when she was small
3 Despite being a millionaire , he lives in a small flat 
4 when does the festive take place ?
5 It is about two kilometres from my home to school
6 he didn't use to ride his bike to school 
7 Despite having a test tomrrow , they are still watching TV now 

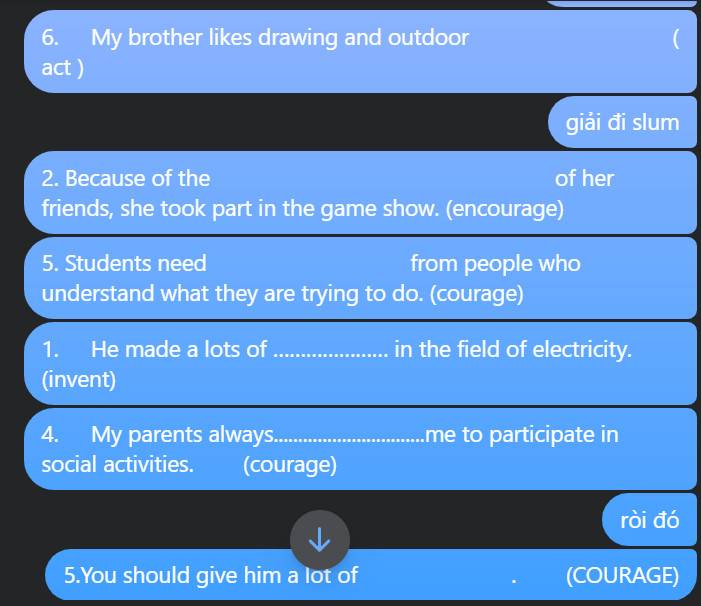
6 activities

2 encouragement

5 encouragement

1 invention

4 encourages

5 encouragement

à bạn ơi, bạn giải thích giùm mình chỗ mấy encouragement đc không ạ. cho mình hỏi là sao không them S vào ạ mình cảm ơn ạ

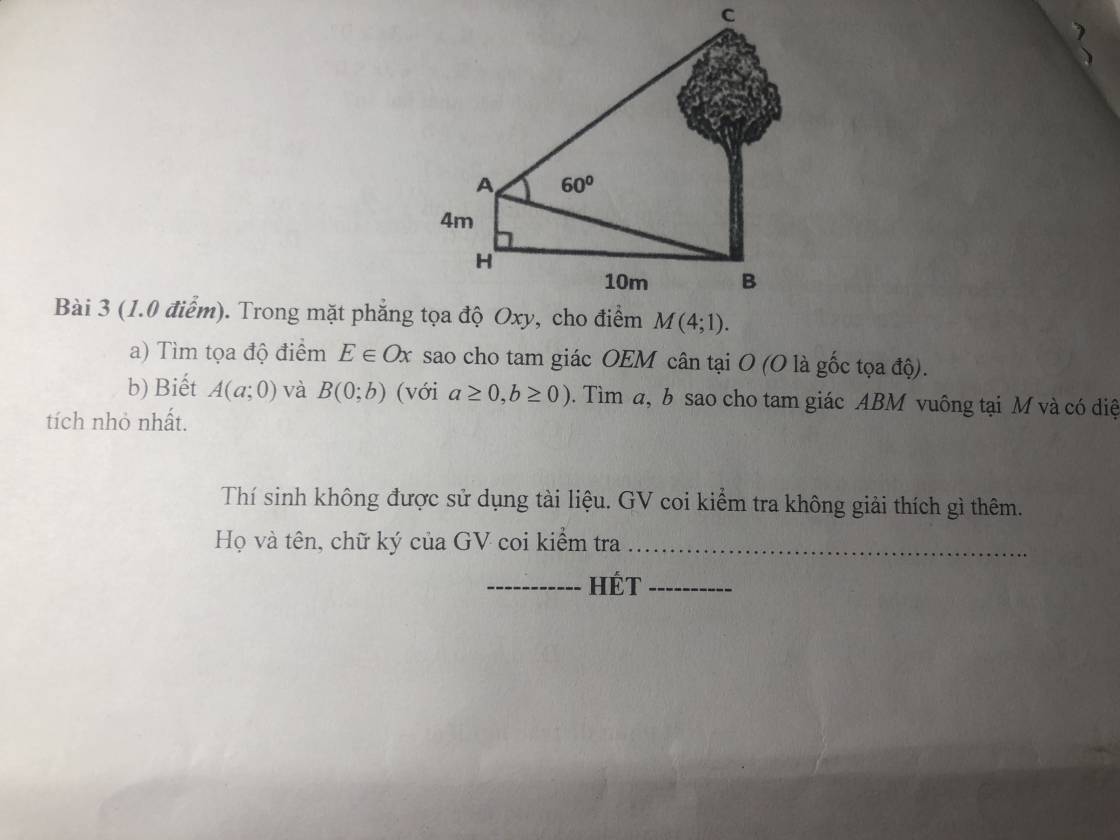
a: E thuộc Ox nên E(x;0)

O(0;0); M(4;1); E(x;0)

\(OM=\sqrt{\left(4-0\right)^2+\left(1-0\right)^2}=\sqrt{17}\)

\(OE=\sqrt{\left(x-0\right)^2+\left(0-0\right)^2}=\sqrt{x^2}=\left|x\right|\)

Để ΔOEM cân tại O thì OE=OM

=>\(\left|x\right|=\sqrt{17}\)

=>\(x=\pm\sqrt{17}\)

2.

Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)

Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)

\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)

 \(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)

Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương

\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)

\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)

\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)

3.

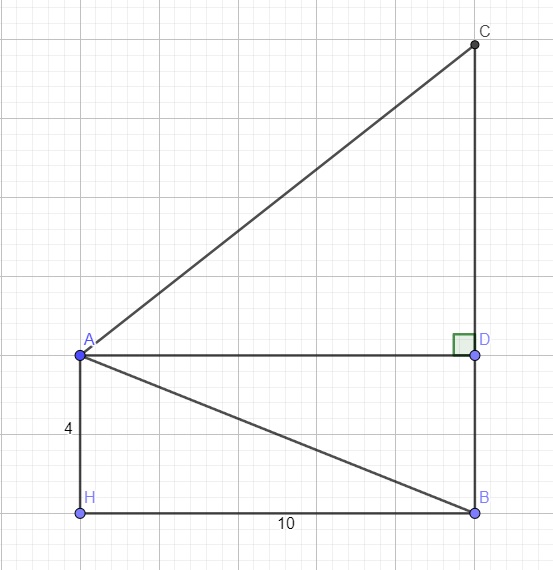
Kẻ AD vuông góc BC tại D

\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)

\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)

\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)

\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)

\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)