Hai cậu bé mỗi người đi một chiếc xe đạp và bắt đầu đi thẳng về phía nhau từ hai nơi cách nhau 20 dặm. Ngay lúc họ bắt đầu, một con ruồi trên tay lái của một chiếc xe đạp bắt đầu bay thẳng về phía chiếc xe đạp kia. Vừa chạm tới tay lái của chiếc xe đạp kia, nó lập tức quay đầu bay về phía sau. Con ruồi bay tới bay lui như thế, bay qua bay lại giữa tay lái của hai chiếc xe đạp cho đến khi hai chiếc xe đạp gặp nhau. Nếu mỗi chiếc xe đạp di chuyển với tốc độ không đổi 5 dặm/h và con ruồi bay với tốc độ không đổi 10 dặm/h thì con ruồi bay tổng cộng bao nhiêu dặm?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mổi người đi xe đạp sẽ phải đi quãng đường 90 dặm. Với vận tốc = 15 dặm/giờ, cần thời gian = 90/15 = 6 giờ. Thời gian con ruồi bay = thời gian của mỗi người đi hết quãng đường 90 dặm = 6 giờ. Vận tốc con ruồi = 30 dặm / giờ. Thời gian bay 6 giờ = 6 x 30 = 180 dặm

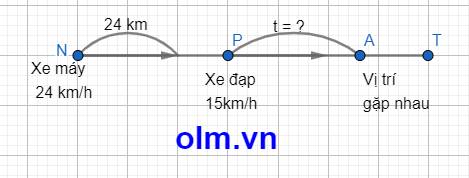
Hiệu vận tốc của xe máy và xe đạp là: 24 - 15 = 9 (km/h)
Thời gian xe máy đuổi kịp xe đạp là: 24 : 9 = \(\dfrac{8}{3}\) (giờ)
Đổi \(\dfrac{8}{3}\) giờ = 2 giờ 40 phút
Đáp số: 2 giờ 40 phút

Gọi VT xe máy là x(x>0)
. VT xe đạp là x-15
Thời gian xe máy là:\(\frac{60+40}{x}=\frac{100}{x}\) (h)
Thời gian xe đạp là :\(\frac{60}{x-15}\)(h)
THeo đề ta có pt:
\(\frac{60}{x-15}=\frac{100}{x}+\frac{2}{3}\) (DO 40p =\(\frac{2}{3}\)h)
\(\Leftrightarrow60.3x=100.3\left(x-15\right)+2x\left(x-15\right)\)
\(\Leftrightarrow180x=300x-4500+2x^2-30x\)
\(\Leftrightarrow2x^2+90x-4500=0\)
Giải Pt ta được \(\orbr{\begin{cases}x=30\left(n\right)\\x=-75\left(l\right)\end{cases}}\)
Vậy Vt xe máy là 30km/h
Vt xe đạp là 30-15=15km/h