Một người đi bộ với tốc độ không đổi 3\(km/h\). Gọi \(s\left( {km} \right)\) là quãng đường đi được trong \(t\) (giờ).
a) Lập công thức tính \(s\) theo \(t\).
b) Vẽ đồ thị của hàm số \(s\) theo biến số \(t\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

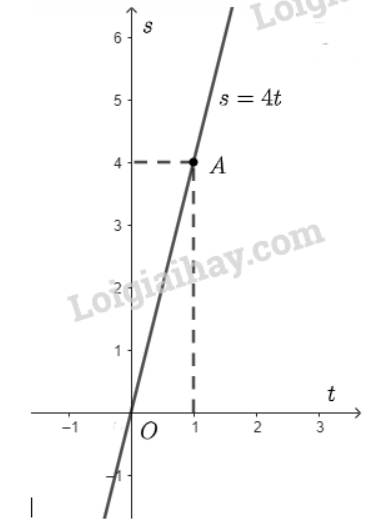
Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).
Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).

Cứ 1 giờ người đó lại đi được \(v\) km.
Cứ 2 giờ người đó lại đi được \(2v\)km.
Vậy sau \(t\left( h \right)\) người đó sẽ đi được quãng đường \(v.t\) km.
Vậy ta có công thức tính \(s\)theo \(t\) như sau: \(s = v.t\) trong đó \(v\) là vận tốc, \(t\) là thời gian và \(s\) là quãng đường đi được.

Ta có:
S = v .t
Trong đó: s: quãng đường đi được
v: vận tốc di chuyển
t: thời gian di chuyển

Ta có:
\(t = \dfrac{s}{v}\)
Trong đó: s: quãng đường đi được
v: vận tốc di chuyển
t: thời gian di chuyển

Ta có các biểu thức:
\(s=vt;v=\dfrac{s}{t};t=\dfrac{s}{v}\)
Tất cả đều là đơn thức không phải đa thức
`S = v.t; v = S/t; t = S/v`.
Không phải là đa thức.

a) s = v.t = 65.t
b) s và t là hai đại lượng tỉ lệ thuận vì s và t liên hệ với nhau theo công thức s = 65t
Hệ số tỉ lệ của s đối với t là: 65
a) Quãng được vật đi được với vận tốc 3 \(km/h\)trong khoảng thời gian \(t\) (giờ) là:
\(s = v.t = 3.t\).
b) Vẽ đồ thị hàm số \(s = 3.t\)
Cho \(t = 1 \Rightarrow s = 3.1 = 3\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(M\left( {1;3} \right)\).
Đồ thị hàm số \(s = 3.t\) là đường thẳng đi qua hai điểm \(O\) và \(M\).