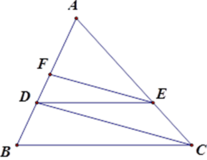
Cho \(\Delta ABC\), một đường thẳng song song với \(BC\) cắt \(AB\) và \(AC\) lần lượt tại \(D\) và \(E\). Qua \(E\) kẻ đường thẳng song song với \(CD\) cắt \(AB\) tại \(F\). Biết \(AB = 25cm,AF = 9cm,EF = 12cm\), độ dài đoạn \(DC\) là
A. 25cm.
B. 20cm.
C. 15cm.
D. 12cm

Chọn B
Chọn đáp án B
Xét tam giác \(ADC\) có \(EF//DC\), theo định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}\) (1)
Xét tam giác \(ABC\) có \(DE//BC\), theo định lí Thales ta có:
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) (2)
Từ (1) và (2) suy ra,
\(\frac{{AF}}{{AD}} = \frac{{AD}}{{AB}} \Rightarrow AF.AB = A{D^2} \Leftrightarrow 9.25 = A{D^2} \Rightarrow AD = \sqrt {9.25} = 15\)
Xét tam giác \(ADC\) có \(EF//DC\), theo hệ quả định lí Thales ta có:
\(\frac{{AF}}{{AD}} = \frac{{EF}}{{DC}} \Rightarrow \frac{9}{{15}} = \frac{{12}}{{DC}} \Leftrightarrow DC = \frac{{12.15}}{9} = 20\)
Vậy \(DC = 20cm\).