Tam giác \(ABC\) có độ dài \(AB = 4cm,AC = 6cm,BC = 9cm.\)Tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác \(A'B'C'\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1A
1
3 tháng 2
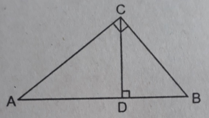
Xét ΔBDA và ΔBAC có
\(\dfrac{BD}{BA}=\dfrac{BA}{BC}\)
\(\widehat{B}\) chung
Do đó: ΔBDA~ΔBAC
=>\(\dfrac{AD}{AC}=\dfrac{BD}{BA}\)
=>\(\dfrac{AD}{5}=\dfrac{4}{6}=\dfrac{2}{3}\)
=>\(AD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)
NT
2
9 tháng 5 2017
a)
ta có t/g ABC cân tại A
->AB=AC=4Cm(đ nghĩa của t/g cân)
b)
chu vi của t/g ABC:
AB +AC+BC
->(4 X 2)+9
->17cm
Vậy chu vi của tam giác ABC là 17cm
(KO CHẮC LÀ ĐÚNG NHA)
HI HI ^ _^
9 tháng 5 2017
giải sai rồi
học bất đẳng thức tam giác chưa AB+AC>BC
cạnh BC - AB< AC<BC + AB
<=>9-4<AC<9+4
<=>5<AC<13
=>AC=9 cm
chu vi tam giác là 9+9+4 =22cm
AH
Akai Haruma
Giáo viên
17 tháng 3 2021
Lời giải:
a) Ta thấy:
$\frac{4}{8}=\frac{5}{10}=\frac{6}{12}$ nên 2 tam giác đồng dạng theo TH c.c.c
b) Pitago: $A'C'=\sqrt{B'C'^2-A'B'^2}=\sqrt{16^2-9^2}=5\sqrt{7}$
Xét tam giác $ABC$ và $A'B'C'$ có:
$\widehat{A}=\widehat{A'}=90^0$
$\frac{AB}{AC}\neq \frac{A'B'}{A'C'}$
Do đó 2 tam giác không đồng dạng
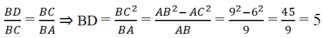
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).