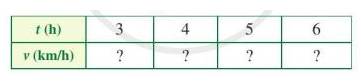
Giả sử một xe ô tô chuyển động đều trên quãng đường AB dài 240 km. Vận tốc v (km/h) và thời gian t (h) của xe ô tô khi đi từ A đến B được liên hệ theo công thức v = \(\frac{{240}}{t}\). Tìm số thích hợp cho trong bảng sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 1:
tóm tắt
\(s=18km=18000m\)
\(t=30'=1800s\)\(=0,5h\)
\(v=?\)
giải
ADCT: \(v=\dfrac{s}{t}\); ta có:
vận tốc của ô tô theo đơn vị km/h là:
\(\dfrac{18}{0,5}=36\left(km/h\right)\)
vận tốc của ô tô theo đơn vị m/s là:
\(\dfrac{18000}{1800}=10\left(m/s\right)\)
bài 2:
tóm tắt
\(s=9000m=9km\)
\(v=45km/h\)
\(t=?\)
giải:
ADCT: \(v=\dfrac{s}{t}\Rightarrow t=\dfrac{s}{v}\); ta có:
thời gian mà xe máy di chuyển hết quãng đường AB là:
\(\dfrac{9}{45}=\dfrac{1}{5}=0,2\left(h\right)\)

Ta có:
\(t = \dfrac{s}{v}\)
Trong đó: s: quãng đường đi được
v: vận tốc di chuyển
t: thời gian di chuyển

Khi v = 40 thì \(t = \dfrac{s}{v} = \dfrac{{180}}{{40}} = 4,5(h)\)
Khi v = 50 thì \(t = \dfrac{s}{v} = \dfrac{{180}}{{50}} = 3,6(h)\)
Khi v = 60 thì \(t = \dfrac{s}{v} = \dfrac{{180}}{{60}} = 3(h)\)
Khi v = 80 thì \(t = \dfrac{s}{v} = \dfrac{{180}}{{80}} = 2,25(h)\)
v (km/h) | 40 | 50 | 60 | 80 |
t (h) | 4,5 | 3,6 | 3 | 2,25 |

Công thức tính quãng đường đi được và phương trình chuyển động
- Của xe máy xuất phát lúc 6 giờ:
s 1 = v 1 t = 40t;
x 1 = s 1 = 40t (với x0 = 0 )
- Của ô tô xuất phát lúc 8 giờ :
s 1 = v 2 (t – 2) = 80(t – 2) với t ≥ 2;
x 2 = x 0 + s 2 = 20 + 80(t – 2)

Thời gian xe đi trên đoạn đg đầu là
`t_1= s_1/v_1=250/50 = 5(h)``
Vận tốc TB trên cả quãng đg là
`v_(tb)=(s_1 +s_2)/(t_1+t_2)=(250+180)/(5+3)=53,75(km//h)`
`b)` khi ngồi trên xe,khi xe đột ngột rẽ sang trái người ta thường bị nghiêng sang bên phải bời vì theo lực quán tính : lúc đầu thì xe và ng c/đ cùng chiều nhưng xe rẽ trái thì theo quán tính thì ng ngồi trên xe sẽ ko thay đổi hg kịp theo xe nên vẫn nghiêng theo hg phải

Ta có:
S = v .t
Trong đó: s: quãng đường đi được
v: vận tốc di chuyển
t: thời gian di chuyển

Gọi thời gian ô tô đi đến nơi 2 xe gặp nhau là x (h) (x >0)
xe máy đi trước ô tô 20 ' =\(\dfrac{1}{3}\)(h) Nên:
Thời gian xe máy đi đến nơi 2 xe gặp nhau là:x +\(\dfrac{1}{3}\) (h)
Quãng đường xe máy đi được : 30.(x+\(\dfrac{1}{3}\)) (km)
Quãng đường Ô tô đi là: 45.x (km)
Vì quãng đường AB dài 90 km , ta có phương trình:
45.x + 30.(x+\(\dfrac{1}{3}\)) = 90
\(\Leftrightarrow\) 75.t = 80 \(\Leftrightarrow\) t = 16/15(h) = 64 (phút)
Vậy sau 64 phút tính theo thời gian ô tô xuất phát thì ô tô gặp xe máy.
Với t = 3 thì v = \(\frac{{240}}{3} = 80\)
Với t = 4 thì v = \(\frac{{240}}{4} = 60\)
Với t = 5 thì v = \(\frac{{240}}{5} = 48\)
Với t = 6 thì v = \(\frac{{240}}{6} = 40\)
t (h)
3
4
5
6
v (km/h)
80
60
48
40