Cho tam giác ABC có AC là cho trọng tâm của tam giác và AB = 15 BC = 18 AC = 27
a) Tính
b) Tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
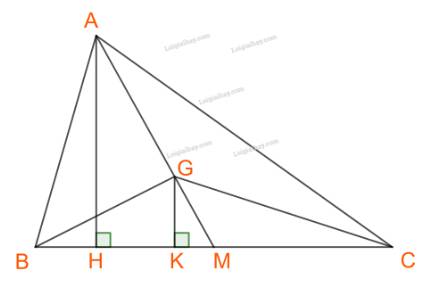
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)

Em tham khảo tại link này nhé.
Câu hỏi của truong nhat linh - Toán lớp 7 - Học toán với OnlineMath

Kéo dài BG cắt AC tại N; CG cắt AB tại M
Có : SAGC = \(\frac{1}{2}\)h.GC ; SBGC = \(\frac{1}{2}\). k. GC mà SAGC = SGBC nên h = k
Mặt khác, SGAM = \(\frac{1}{2}\)h.GM ; SGBM = \(\frac{1}{2}\)k. GM
=> SGAM = SGBM
Lại có : tam giác GAM; GBM đều chung chiều cao hạ từ G xuống AB => đáy MA = MB => M là trung điểm của AB => CM là trung tuyến
+) Tương tự, từ SGAB = SGBC => N là trung điểm của AC => BN là trung tuyến
BN cắt CM tại G => G là trọng tâm tam giác ABC