Tìm GTNN của biểu thức sau:
2x2 -10x +1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự

Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
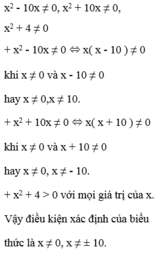

Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:



|2-2x^2|>=0
=>-2|2x^2-2|<=0
=>-2|2x^2-2|+1<=1
Dấu = xảy ra khi 2x^2-2=0
=>x^2=1
=>x=1 hoặc x=-1

a: Ta có: \(A=2x^2-8x+1\)
\(=2\left(x^2-4x+\dfrac{1}{2}\right)\)
\(=2\left(x^2-4x+4-\dfrac{7}{2}\right)\)
\(=2\left(x-2\right)^2-7\ge-7\forall x\)
Dấu '=' xảy ra khi x=2

Với x = 20040, ta có: A = 10/20040 = 1/2004.
Vậy A = 1/2004 khi x = 20040.
\(=2\left(x^2-5x+\frac{1}{2}\right)=2\left(x^2-5x+\frac{25}{4}-\frac{23}{4}\right)=2\left[\left(x-\frac{5}{2}\right)^2-\frac{23}{4}\right]=2\left(x-\frac{5}{2}\right)^2-\frac{23}{2}\)
Suy ra giá trị nhỏ nhất của biểu thức trên là -23/2 khi x=5/2