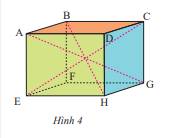
Cho hình hộp chữ nhật ABCD. EFGH (Hình 4) có AD = 8 cm, DC = 5 cm, DH = 6,5 cm. Tìm độ dài các cạnh AB, FG, AE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là: | D. Hình vuông. |
A. 4cm. B. 7cm. C. 14cm. Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là: | D. 8cm. |
A. 10cm. B. 15cm. C. 5cm. | D. 8cm. |
Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. D. Hình vuông.
Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
A. 4cm. B. 7 cm. C. 14cm. D. 8cm.
Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là:
A. 10cm. B. 15cm. C. 5cm. D. 8 cm

S_EFGH = S_ABCD - S_BGF - S_GCH - S_AEHD
Là các hình tam giác vuông và hình thang vuông, dễ dàng tìm được hàm diện tích của EFGH theo x: -2x2 + 32.5x
Nếu được thì đạo hàm là tìm được giá trị x mà S max.

Ta có: \(\dfrac{AD}{AB}=\dfrac{8}{15}\)
nên \(AD=\dfrac{8}{15}AB\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow\left(\dfrac{8}{15}AB\right)^2+AB^2=68^2=4624\)
\(\Leftrightarrow AB^2\cdot\dfrac{289}{225}=4624\)
\(\Leftrightarrow AB^2=3600\)
\(\Leftrightarrow AB=60\left(cm\right)\)
\(\Leftrightarrow AD=\dfrac{8}{15}AB=\dfrac{8}{15}\cdot60=32\left(cm\right)\)
\(\Leftrightarrow CD=60cm;BC=32cm\)
Ta có: AB = DC = EF = HG, mà DC = 5 cm nên AB = 5 cm
AD = BC = FG = EH, mà AD = 8 cm nên FG = 8 cm
AE = FB = DH = CG, mà DH = 6,5 cm nên AE = 6,5 cm