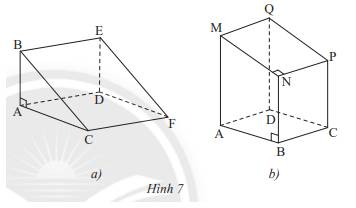
Quan sát hai hình lăng trụ đứng trong Hình 7.
a) Chỉ ra mặt đáy và mặt bên của mỗi hình lăng trụ
b) Ở hình 7a, cạnh BE bằng các cạnh nào? Ở hình 7b, cạnh MQ bằng các cạnh nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các mặt đáy là: ABCD, EFGH
Các mặt bên là: ABFE; ADHE; CDHG; BCGF
b) Các cạnh bên là: AE;BF;CG;DH

+ 2 mặt đáy : ABC, MNP
+ 3 mặt bên : ACPM, BAMN, BCPN
+ Cạnh đáy : NM, MP, NP, AB, BC, CA
+ Cạnh bên : AM, BN, CP

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh

| Hình | a | b | c | d |
| Số cạnh của một đáy | 3 | 4 | 6 | 5 |
| Số mặt bên | 3 | 4 | 6 | 5 |
| Số đỉnh | 6 | 8 | 12 | 10 |
| Số cạnh bên | 3 | 4 | 6 | 5 |

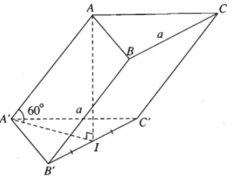
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
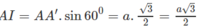
b) 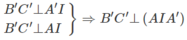
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)

Hình lăng trụ đứng tứ giác ABCD. A’B’C’D’ có:
+) 6 mặt gồm: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
+) 12 cạnh gồm: AB; BC;CD;DA;A’B’;B’C’;C’D’; D’A’; AA’; BB’; CC’ ; DD’.
+) 8 đỉnh gồm: A;B;C;D;A’;B’;C’;D’.

a) Đáy dưới ABC và đáy trên A’B’C’ là hình tam giác
b) Mặt bên AA’C’C là hình chữ nhật
c) Hai cạnh bên AA’ và CC’ có độ dài bằng nhau

Hình lăng trụ đứng tam giác có:
+) 5 mặt gồm: ABC; A’B’C’; ABB’A’; BCC’B’; ACC’A’
+) 9 cạnh gồm: AB; BC;CA;A’B’;B’C’;C’A’; AA’; BB’; CC’
+) 6 đỉnh gồm: A;B;C; A’;B’;C’.
a) Hình 7a: Mặt đáy: ABC và DEF
Mặt bên: ABED, BCFE, ACFD
Hình 7b: Mặt đáy: ABCD, MNPQ
Mặt bên: ABNM, BCPN, CDQP, ADQM.
b) Ở Hình 7a, cạnh BE = AD = CF
Ở Hình 7b, cạnh MQ = NP = BC = AD