Lương trung bình tháng của công nhân ở một xí nghiệp vào năm thứ n tính từ năm 2015 được tính bởi biểu thức \(C{(1 + 0,04)^n}\), trong đó C = 5 triệu đồng. Hãy tính lương trung bình tháng của công nhân xí nghiệp đó vào năm 2020 (ứng với n = 5).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 1 2019
Đáp án A
Từ quý I năm 2017 đến hết quý IV năm 2022 là 24 quý.
Tổng lương chính là tổng của cấp ố cộng với
CM
9 tháng 11 2019
Đến năm thứ 16 thì người đó được tăng lương số lần là: 16 3 = 5 lần.
Áp dụng công thức: S n = A 1 + r n ta có số tiền người đó nhận được ở tháng đầu tiên của năm thứ 16 là:
6 ( 1 + 10 % ) 5 = 6 . 1 . 1 5 triệu đồng
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
7 tháng 11 2023
Sau 5 năm lương tăng số lần:
5 x 3 = 15 (lần)
Tổng lương sau 5 năm:
15 x 500 000 + 4 000 000 = 11 500 000 (đồng)
Đ.số:...
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Nhà máy A:
+) Số trung bình: \(\overline x = \frac{{4 + 5 + 5 + 47 + 5 + 6 + 4 + 4}}{8} = 10\)
+) Mốt: \({M_o} = 4,{M_o} = 5\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 4; 4; 4; 5; 5; 5; 6; 47.
\({Q_2} = {M_e} = 5\)
\({Q_1}\) là trung vị của nửa số liệu: 4; 4; 4; 5. Do đó \({Q_1} = 4\)
\({Q_3}\) là trung vị của nửa số liệu: 5; 5; 6; 47. Do đó \({Q_3} = 5,5\)
+) Phương sai \({S^2} = \frac{1}{8}\left( {{4^2} + {5^2} + ... + {4^2}} \right) - {10^2} = 196\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 14\)
Nhà máy B:
+) Số trung bình: \(\overline x = \frac{{2 + 9 + 9 + 8 + 10 + 9 + 9 + 11 + 9}}{9} = 8,4\)
+) Mốt: \({M_o} = 9\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 8; 9; 9; 9; 9; 9; 10; 11
\({Q_2} = {M_e} = 9\)
\({Q_1}\) là trung vị của nửa số liệu: 2; 8; 9; 9. Do đó \({Q_1} = 8,5\)
\({Q_3}\) là trung vị của nửa số liệu: 9; 9; 10; 11. Do đó \({Q_3} = 9,5\)
+) Phương sai \({S^2} = \frac{1}{9}\left( {{2^2} + {9^2} + ... + {9^2}} \right) - 8,{4^2} = 6,55\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 2,56\)
b)
Nhà máy A có: \({\Delta _Q} = 1,5\)
Vậy giá trị ngoại lệ \(x > 5,5 + 1,5.1,5 = 7,75\) hoặc \(x < 4 - 1,5.1,5 = 1,75\) là 47.
Nhà máy B có: \({\Delta _Q} = 1\)
Vậy giá trị ngoại lệ \(x > 9,5 + 1,5.1 = 11\) hoặc \(x < 8,5 - 1,5.1 = 7\) là 2.
Ta so sánh trung vị: \(9 > 5\), do dó công nhân nhà máy B có mức lương cao hơn.
Chú ý
Ta không so sánh số trung bình vì có giá trị 47 quá lớn so với các giá trị còn lại.
NN
NGUYEN NAM HAI
VIP
17 tháng 2
lần lượt các ngày thứ 7 tiếp theo là 9\5 ; 16\5 ; 23\5 ; 30\5 nên có 5 ngày thứ 7. vì vậy :
Anh Bình kiếm được số tiền là:
200.000 nhân 5 = 2000000 [ đồng ]
ĐS : 2000000 đồng
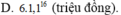
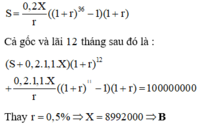
Ta có công thức tính lương là : \(C{(1 + 0,04)^n}\)
Ta thay C = 5 và n = 5 vào công thức, ta có : \(5.{(1 + 0,04)^5} = 5.1,{04^5} \approx 6,08\) (triệu đồng)
Vậy lương trung bình của công nhân năm 2020 là 6,08 triệu đồng.