Chọn D.

Ta có nhận xét như sau:

Ta có:

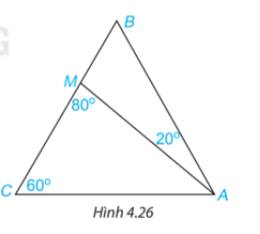
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)

\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)

Áp dụng định lí tổng ba góc trong một tam giác:

+) Trong tam giác AMB có:

\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)

+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)

a) \(cos638^o=cos\left(-82^o\right)=cos\left(82^o\right)=sin8^o\)

b) \(cot\dfrac{19\pi}{5}=cot\dfrac{4\pi}{5}=-cot\dfrac{\pi}{5}\)

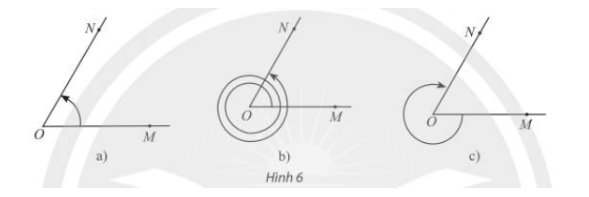
a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)

b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)

c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)

Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)

a) Ta có:

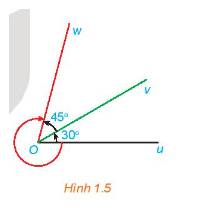
- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là

sđ\((Ou,Ov) =  {30^ \circ } + n{.360^ \circ }\)

- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là

sđ \((Ov,Ow) =  {45^ \circ } + m{.360^ \circ }\)

- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là

sđ \((Ou,Ow) =  {75^ \circ } + k{.360^ \circ }\)

b) Với các góc lượng giác ở câu a, ta có:

\(sđ(Ou,Ov) +sđ (Ov,Ow)\)

\(  =  {30^ \circ } + n{.360^ \circ } + {45^ \circ } + m{.360^ \circ } \)

\(= {75^ \circ } + (n+m){.360^ \circ } \)

\(= {75^ \circ } + k{.360^ \circ = sđ (Ou,Ow)} \)

với  k = n + m

Ta có:

\((O'u',O'v') = (Ou,Ov) + k2\pi \,\, = \, - \frac{{4\pi }}{3}\, + k2\pi \,\,\,\,\,\,\,\,(k \in \mathbb{Z})\)

Tham khảo:

a: 

b: 

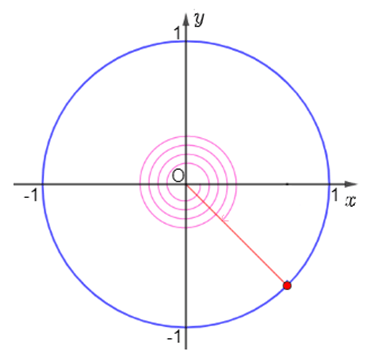
a) Ta có \( - {1485^ \circ } =  - {45^ \circ } + ( - 4){.360^ \circ }\). Vậy điểm biểu diễn góc lượng giác có số đo \( - {1485^ \circ }\)là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho \(\widehat {AMO} = {45^ \circ }\)

b) Ta có \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \). Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{4}\) là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho \(\widehat {AMO} = \frac{{3\pi }}{4}\).