Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T= 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã).(Nguồn: Đại số và Giải tích 11, NXBGD Việt Nam, 2021)Gọi \({u_n}\) là khối lượng chất phóng xạ còn lại sau chu kì thứ n. a) Tìm số hạng tổng quát \({u_n}\) của dãy số \(\left( {{u_n}}...
Đọc tiếp
Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T= 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã).
(Nguồn: Đại số và Giải tích 11, NXBGD Việt Nam, 2021)
Gọi \({u_n}\) là khối lượng chất phóng xạ còn lại sau chu kì thứ n.
a) Tìm số hạng tổng quát \({u_n}\) của dãy số \(\left( {{u_n}} \right)\).
b) Chứng minh rằng \(\left( {{u_n}} \right)\) có giới hạn là 0.
c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \({10^{ - 6}}\) g.
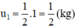
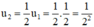
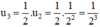
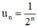
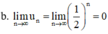
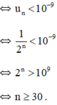
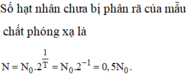
a) Sau một chu kì bán rã \({u_1} = 1.\frac{1}{2} = \frac{1}{2}\left( {kg} \right)\)
Sau hai chu kì bán rã \({u_2} = \frac{1}{2}.{u_1} = \frac{1}{{{2^2}}}\left( {kg} \right)\)
…
Vậy sau n chu kì bán rã \({u_n} = \frac{1}{{{2^n}}}\)
b) \(\lim {u_n} = \lim \frac{1}{{{2^n}}} = \lim {\left( {\frac{1}{2}} \right)^n} = 0\)
c) Đổi \({10^{ - 6}}g = {10^{ - 9}}kg\)
Vì chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \({10^{ - 6}}\) g nên ta có
\({u_n} < {10^{ - 9}} \Leftrightarrow \frac{1}{{{2^n}}} < {10^{ - 9}} \Leftrightarrow {2^n} > {10^9} \Leftrightarrow n > {\log _2}{10^9} \approx 29,9\)
Vậy sau 30 chu kì là 30.24 000 = 720 000 năm thì khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người.