GIÚP MÌNH VỚI MỌI NGƯỜI ƠI. GIẢI CHI TIẾT HỘ MÌNH NHÉ! CẢM ƠN NHIỀU.

a) Xét ΔABM và ΔFCM có 

AM=FM(gt)

\(\widehat{AMB}=\widehat{FMC}\)(hai góc đối đỉnh)

BM=CM(M là trung điểm của BC)

Do đó: ΔABM=ΔFCM(c-g-c)

b) Xét ΔBMF và ΔCMA có 

BM=CM(M là trung điểm của BC)

\(\widehat{BMF}=\widehat{CMA}\)(hai góc đối đỉnh)

FM=AM(gt)

Do đó: ΔBMF=ΔCMA(c-g-c)

nên \(\widehat{FBM}=\widehat{ACM}\)(hai góc tương ứng)

mà \(\widehat{FBM}\) và \(\widehat{ACM}\) là hai góc ở vị trí so le trong

nên BF//AC(Dấu hiệu nhận biết hai đường thẳng song song)

Ta có: ΔABM=ΔFCM(cmt)

nên \(\widehat{ABM}=\widehat{FCM}\)(hai góc tương ứng)

mà \(\widehat{ABM}\) và \(\widehat{FCM}\) là hai góc ở vị trí so le trong

nên AB//CF(Dấu hiệu nhận biết hai đường thẳng song song)

cậu ơi nhầm bài nào vậy ạ? ;-;

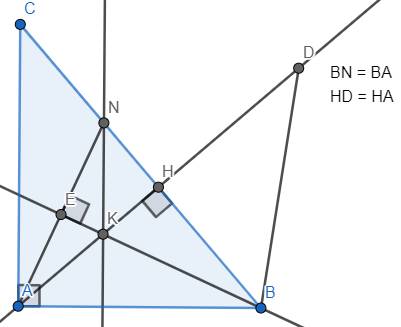
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:

- BE là cạnh chung, BN = BA (giả thuyết)

Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)

b) Theo đề ta có BH vuông góc với AD và HA = HD

Suy ra BH là đường trung trực của AD

Suy ra BA = BD (vì B nằm trên đường trung trực của AD)

c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K

Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB

Mà AC cũng vuông góc với AB, suy ra NK // CA

a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
     tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
    + Chung BE
    + BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh  góc vuông)

b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
     tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
    + Chung BH
    + HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
    => BA = BD (2 cạnh tương ứng)

tham khảo nhé . 

 gọi K là giao điểm của ED và BC , vẽ DM vuông góc với AH ở M. 
Ta có DM // BC ( tự cm ) => MD /CH = AD / AC = AM / AH = 1 / 3 ( do AD = 1/3 AC ) 
=> MD = CH/3 ( * ) và AM = AH/3 = EH ( do EH = AH/3 ) 
ta có AM = EH /3 => AM = MH / 2 = EH => EH = EM / 3
ta lại có HK / MD = EH / EM = 1/ 3 ( ** ) 
từ ( *) và ( ** ) ta có HK = CH / 9 . 
ta có AH^2 = BH.CH = 9 (EH^2) = BH.9HK 
=> EH^2 = BH.HK => tam giác BEK vuông ở E mà D thuộc EK nên BÊD = 90. 

*Kẻ DM ⊥ AH ( M ∈ AH )
 Xét △AHC có : MD // BC 
=> AM/AH = AD/AC ( Ta-lét)
=> AM/AH=HE/AH ( = AD/AC = 1/3 )
=> AM = HE
 Ta có : AH + HE - AM = MH => AH = MH
 Xét △EMD ( góc EMD = 90 ) 
=> ME^2 + MD^2 = DE^2 ( Pytago )                             (1)
Tương tự với các : +△BHE => BE^2 = BH^2 + HE^2   (2)
                              +△ABH => BH^2 = AB^2 - AH^2
                              +△AMD => MD^2 = AD^2 - AM^2
                              +△ABD => BD^2 = AB^2 + AD^2
Cộng (1) với (2), ta đc : 
   DE^2 + BE^2 = ME^2 + MD^2 + BH^2 - HE^2
<=> DE^2 + BE^2 = AH^2 + AD^2 - AM^2 + AB^2- AH^2 + AM^2
<=> DE^2 + BE^2 = AD^2 + AB^2
=> DE^2 + BE^2 = BD^2
=> △BDE vuông tại E ( Pytago đảo )
=> góc BED = 90 -> đcpcm
( Có thể có sai sót lúc làm mong đóng góp ) =))

a: Xét tứ giác ABEC có 

M là trung điểm của AE

M là trung điểm của BC

Do đó: ABEC là hình bình hành

mà \(\widehat{CAB}=90^0\)

nên ABEC là hình chữ nhật

Suy ra: CD⊥AC

b: Xét ΔCAE có 

CH là đường cao

CH là đường trung tuyến

Do đó: ΔCAE cân tại C

c: Ta có: ΔCAE cân tại C

nên CA=CE

mà CA=BD

nên BD=CE

d: Xét ΔMAE có 

MH là đường cao

MH là đường trung tuyến

Do đó: ΔMAE cân tại M

Xét ΔDEA có 

EM là đường trung tuyến

EM=DA/2

Do đó: ΔDEA vuông tại E

hay AE⊥ED

a) xét tam giác AHB và tam giác AHD ta có

AH=AH ( cạnh chung)

BH=HD(gt)

góc AHB= góc AHD (=90)

-> tam giác AHB= tam giác AHD (c-g-c)

b) ta có

DE vuông góc AC (gt)

AB vuông góc AC ( tam giác ABC vuông tại A)

-> DE//AB

ta có

AC>AB (gt)

-> góc ABC > góc ACB ( quan hệ cạnh góc đối diện trong tam giác)

c) Xét tam giác AHB và tam giác IHD ta có

AH=HI (gt)
BH=HD(gt)

góc AHB= góc IHD (=90)

-> tam giac AHB = tam giác IHD (c-g-c)

-> góc BAH= góc HID ( 2 góc tương ứng )

mà 2 góc nẳm ở vị trí sole trong 

nên BA//ID

ta có

BA//ID (cmt)

BA//DE (cm b)

-> ID trùng DE

-> I,E,D thẳng hàng