Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
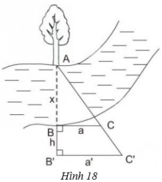
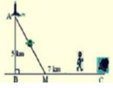
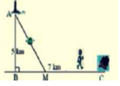
Từ vị trí A, đo góc nghiêng \(\alpha\) so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng \(\beta\) so với bờ biển tới vị trí C đã chọn (Hình 18).
Bằng cách giải tam giác ABC,họ tính được khoảng cách AC.
Giải tam giác được hiểu như thế nào?

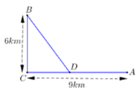





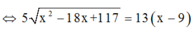
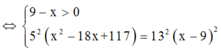


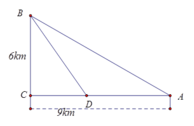
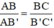 (hệ quả định lý Talet)
(hệ quả định lý Talet)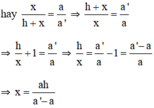
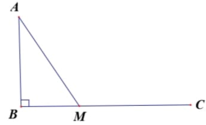

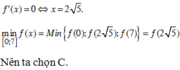
Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Mà \(AB=d, \hat {B} =\beta; \hat {C} =180^o-\alpha -\beta \)
\(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)