Hãy chọn ngẫu nhiên trong lớp ra 5 bạn nam và 5 bạn nữ rồi do chiều cao các bạn đó. So sánh xem chiều cao của các bạn năm hay các bạn nữ đồng đều hơn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
Không gian mẫu có số phần tử là ![]() .
.
Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: ![]() .
.
Vậy xác suất cần tính là 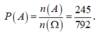 .
.

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có ![]() cách chọn
cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có ![]() cách chọn
cách chọn
Suy ra xác suất cần tính bằng 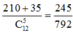

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2 = 210 cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1 = 35 cách chọn
Suy ra xác suất cần tính bằng
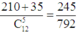

Tổng chiều cao 8 bạn:
(5 + 2) x 145 + 129= 1144(cm)
Trung bình số đo chiều cao của 5 bạn nam và 3 bạn nữ là:
1144: (5+3)= 143(cm)
Đ.số: 143cm

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{45}^2.C_{45}^2\)
a) Gọi A là biến cố “Trong 4 bạn được chọn có ít nhất 1 bạn nam”, ta có biến cố đối \(\overline A \): “Trong 4 bạn được chọn không có bạn nam nào”
\(\overline A \) xảy ra khi các bạn được chọn đều là nữ. Số kết quả thuận lợi cho biến cố \(\overline A \) là \(n\left( {\overline A } \right) = C_{20}^2.C_{24}^2\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{C_{20}^2.C_{24}^2}}{{C_{45}^2.C_{45}^2}} = \frac{{874}}{{16335}}\)
Suy ra, xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{874}}{{16335}} = \frac{{15461}}{{16335}}\)
b) Gọi A là biến cố “Trong 4 bạn được chọn có đủ cả nam và nữ” ta có biến cố đối \(\overline A \): “Trong 4 bạn được chọn đều là nữ hoặc đều là nam”
\(\overline A \) xảy ra khi các bạn được chọn đều là nữ hoặc nam. Số kết quả thuận lợi cho biến cố \(\overline A \) là \(n\left( {\overline A } \right) = C_{20}^2.C_{24}^2 + C_{25}^2.C_{21}^2\)
Xác suất của biến cố \(\overline A \) là \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{C_{20}^2.C_{24}^2 + C_{25}^2.C_{21}^2}}{{C_{45}^2.C_{45}^2}} = \frac{{1924}}{{16335}}\)
Suy ra, xác suất của biến cố A là \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{1924}}{{16335}} = \frac{{14411}}{{16335}}\)

Gọi A là biến cố: “5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ “
- Số phần tử của không gian mẫu: Ω = C 15 5 .
-Số cách chọn 5 bạn trong đó có 4 nam, 1 nữ là: C 8 4 . C 7 1 .
- Số cách chọn 5 bạn trong đó có 3 nam, 2 nữ là: C 8 3 . C 7 2 .
Số cách chọn 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
n A = C 8 4 . C 7 1 + C 8 3 . C 7 2 = 1666
Xác suất để 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
P A = n A Ω = 1666 C 15 5 = 238 429 .
Chọn đáp án B.

Số cách chọn các bạn đi lao động là:
![]()
Gọi biến cố A: “Chọn mỗi tổ 2 bạn đi lao động, trong đó có đúng 3 bạn nữ”.
Khi đó ta có các TH sau:
+) Tổ 1 có 2 bạn nữ, tổ 2 có 1 bạn nữ và 1 bạn nam có:
![]()
+) Tổ 1 có 1 bạn nữ và 1 bạn nam, tổ 2 có 2 bạn nữ có:
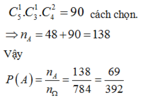
Chọn B.

Chọn B
Chọn mỗi tổ 2 bạn nên số phần tử của không gian mẫu ![]() .
.
Gọi A là biến cố : “Có đúng 3 bạn nữ trong 4 bạn đi lao động”, khi đó
TH1: Chọn 2 nữ tổ I, 1 nữ tổ II, 1 nam tổ II có ![]() .
.
TH2: Chọn 2 nữ tổ II, 1 nữ tổ I, 1 nam tổ I có ![]() .
.
Suy ra ![]() .
.
Xác suất để chọn 4 bạn đi lao động có đúng 3 bạn nữ là ![]() .
.

Chiều cao 5 HS nam
170
164
172
168
176
Chiều cao 5 HS nữ
155
152
157
162
160
+) Khoảng biến thiên chiều cao của các học sinh nam là: \(176 - 164 = 12\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \(164,168,170,172,176\)
Bước 2: \(n = 5\), là số lẻ nên \({Q_2} = {M_e} = 170\)
\({Q_1}\) là trung vị của nửa số liệu \(164,168\). Do đó \({Q_1} = \frac{1}{2}(164 + 168) = 166\)
\({Q_3}\) là trung vị của nửa số liệu \(172,176\). Do đó \({Q_3} = \frac{1}{2}(172 + 176) = 174\)
Khoảng tứ phân vị \({\Delta _Q} = 174 - 166 = 8\)
+) Khoảng biến thiên chiều cao của các học sinh nữ là: \(162 - 152 = 10\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \(152,155,157,160,162\)
Bước 2: \(n = 5\), là số lẻ nên \({Q_2} = {M_e} = 157\)
\({Q_1}\) là trung vị của nửa số liệu \(152,155\). Do đó \({Q_1} = \frac{1}{2}(152 + 155) = 153,5\)
\({Q_3}\) là trung vị của nửa số liệu \(160,162\). Do đó \({Q_3} = \frac{1}{2}(160 + 162) = 161\)
Khoảng tứ phân vị \({\Delta _Q} = 161 - 153,5 = 7,5\)
Kết luận: So sánh khoảng biến thiên hay tứ phân vị thì theo mẫu số liệu trên, chiều cao của 5 bạn nữ là đồng đều hơn.