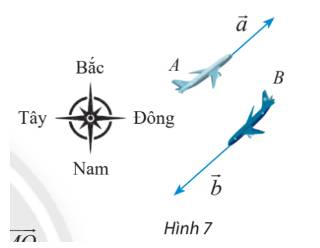
Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc \(30^\circ \) (hình 7)
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD
b) Biểu diễn vận tốc \(\overrightarrow v \) theo hai vectơ và \(\overrightarrow j \)
c) Tìm tọa độ của \(\overrightarrow v \)


a) Vận tốc 240 km/h nên \(\left| {\overrightarrow v } \right| = AC = 240\)
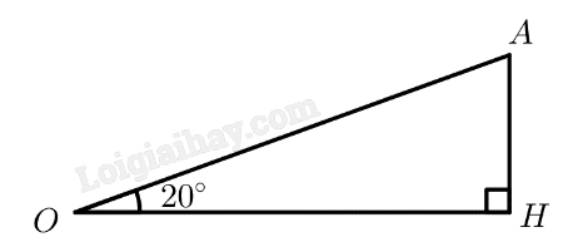
Áp dụng các tính chất trong tam giác vuông ta có
\(AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120{\sqrt 3 }\)
\(AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120\)
b) Xem A là gốc tọa độ nên ta có \(\overrightarrow {AB} = 120\overrightarrow i ,\overrightarrow {AD} = 120{\sqrt 3 }\overrightarrow j ,\overrightarrow v = \overrightarrow {AC} = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
c)
Ta có \(\overrightarrow v = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow v \) là \(\left( {120;120{\sqrt 3 }} \right)\)