Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1;- 2), N(4;- 1) và P(6 ; 2) lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm toạ độ của các điểm A, B, C.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = - 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = - 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { - 1; - 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { - 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { - 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.

Chọn A
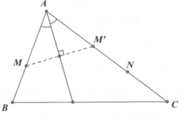
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.




Đáp án A
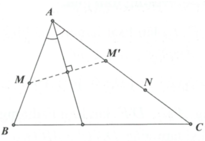
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Hướng dẫn giải.
Gọi M ' ∈ A C là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.
Phương trình MM’ là: 3 x + y - 11 = 0
Toạ độ điểm I là nghiệm của hệ:
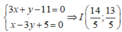
M’ đối xứng với M qua
![]()
Đường thẳng AC qua N và M’ nên có phương trình:
![]()
Tọa độ A là nghiệm của hệ:
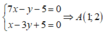
Đường thẳng AB đi qua A, M nên có phương trình:
x + y - 3 = 0
Gọi
![]()
Do G là trọng tâm tam giác ABC nên ta có:
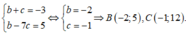
Vậy tọa độ các đỉnh của tam giác ABC là:
![]()

Do C thuộc trục tung nên tọa độ có dạng \(C\left(0;c\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;-1\right)\\\overrightarrow{AC}=\left(-1;c-2\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại A \(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow4-\left(c-2\right)=0\Rightarrow c=6\)
\(\Rightarrow C\left(0;6\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-1;4\right)\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{\left(-4\right)^2+\left(-1\right)^2}=\sqrt{17}\\AC=\sqrt{\left(-1\right)^2+4^2}=\sqrt{17}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{17}{2}\)

Gọi E(x;y) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-2\right)\\\overrightarrow{EC}=\left(3-x;3-y\right)\end{matrix}\right.\)
Tứ giác ABCE là hbh khi \(\overrightarrow{AB}=\overrightarrow{EC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-x=1\\3-y=-2\end{matrix}\right.\) \(\Rightarrow E\left(2;5\right)\)

1: \(\overrightarrow{AB}=\left(-10;-5\right)\)
\(\overrightarrow{AC}=\left(-6;3\right)\)
\(\overrightarrow{BC}=\left(4;8\right)\)
Vì \(\overrightarrow{AC}\cdot\overrightarrow{BC}=0\) ΔABC vuông tại C
\(AC=\sqrt{\left(-6\right)^2+3^2}=3\sqrt{5}\)
\(BC=\sqrt{4^2+8^2}=4\sqrt{5}\)
Do đó: \(S_{ABC}=\dfrac{AC\cdot BC}{2}=\dfrac{3\sqrt{5}\cdot4\sqrt{5}}{2}=3\sqrt{5}\cdot2\sqrt{5}=30\)

Do C thuôc trục hoành nên tọa độ có dạng \(C\left(c;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(c+2;-4\right)\\\overrightarrow{BC}=\left(c-8;-4\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại C \(\Rightarrow\overrightarrow{AC}.\overrightarrow{BC}=0\)
\(\Rightarrow\left(c+2\right)\left(c-8\right)+16=0\)
\(\Rightarrow c^2-6c=0\Rightarrow\left[{}\begin{matrix}c=0\\c=6\end{matrix}\right.\)
Vậy có 2 điểm C thỏa mãn là \(C\left(0;0\right)\) và \(C\left(6;0\right)\)

\(\overrightarrow{AB}=\left(4;2\right)=2\left(2;1\right)\Rightarrow AB=2\sqrt{5}\)
Đường thẳng AB nhận (1;-2) là 1 vtpt nên pt có dạng:
\(1\left(x+1\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+5=0\)
\(\overrightarrow{AC}=\left(2;-8\right)=2\left(1;-4\right)\Rightarrow AC=2\sqrt{17}\)
Đường thẳng AC nhận (4;1) là 1 vtpt nên pt có dạng:
\(4\left(x+1\right)+1\left(y-2\right)=0\Leftrightarrow4x+y+2=0\)
Gọi \(M\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}S_{MAB}=\dfrac{1}{2}d\left(M;AB\right).AB\\S_{MAC}=\dfrac{1}{2}d\left(M;AC\right).AC\end{matrix}\right.\)
\(S_{MAB}=S_{MAC}=d\left(M;AB\right).AB=d\left(M;AC\right).AC\)
\(\Leftrightarrow\dfrac{\left|x-2y+5\right|}{\sqrt{1+\left(-2\right)^2}}.2\sqrt{5}=\dfrac{\left|4x+y+2\right|}{\sqrt{4^2+1^2}}.2\sqrt{17}\)
\(\Leftrightarrow\left|x-2y+5\right|=\left|4x+y+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+y+2=x-2y+5\\4x+y+2=-x+2y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y-1=0\\5x-y+7=0\end{matrix}\right.\)
Vậy quỹ tích M là 2 đường thẳng có pt: \(\left[{}\begin{matrix}x+y-1=0\\5x-y+7=0\end{matrix}\right.\)
Theo tích chất đường trung bình trong một tam giác ta có: \(\overrightarrow {PN} = \overrightarrow {BM} = \overrightarrow {MC} \) và \(\overrightarrow {MP} = \overrightarrow {NA} \)
Gọi \(A\left( {{a_1},{a_2}} \right),B\left( {{b_1};{b_2}} \right),C\left( {{c_1};{c_2}} \right)\)
Ta có: \(\overrightarrow {PN} = \left( {2;3} \right)\),\(\overrightarrow {BM} = \left( {1 - {b_1}; - 2 - {b_2}} \right)\), \(\overrightarrow {MC} = \left( {{c_1} - 1;{c_2} + 2} \right)\), \(\overrightarrow {MP} = \left( {5;4} \right)\), \(\overrightarrow {NA} = \left( {{a_1} - 4;{a_2} + 1} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {BM} \Leftrightarrow \left\{ \begin{array}{l}2 = 1 - {b_1}\\3 = - 2 - {b_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b_1} = - 1\\{b_2} = - 5\end{array} \right.\) .Vậy \(B\left( { - 1; - 5} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {MC} \Leftrightarrow \left\{ \begin{array}{l}2 = {c_1} - 1\\3 = {c_2} + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{c_1} = 3\\{c_2} = 1\end{array} \right.\) .Vậy \(C\left( {3;1} \right)\)
Có \(\overrightarrow {NA} = \overrightarrow {MP} \Leftrightarrow \left\{ \begin{array}{l}5 = {a_1} - 4\\4 = {a_2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a_1} = 9\\{a_2} = 3\end{array} \right.\) .Vậy \(A\left( {9;3} \right)\)