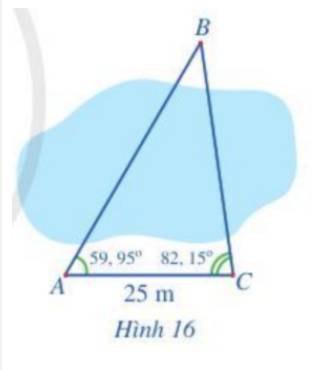
người ta dự định bắc một cái cầu qua một con sông. Để đo khoảng cách giữa hai đầu A và B của cầu kĩ sư làm như sau. Một người đứng ở vị trí A, một người đứng ở vị trí C dọc trên cùng một bờ và tiến hành đo đạc. Kết quả đo được là khoảng cách AC=25m, góc BAC= 59 độ, góc BCA= 82 độ. Em hãy giúp kĩ sư tính khoảng cách giữa hai đầu cầu nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

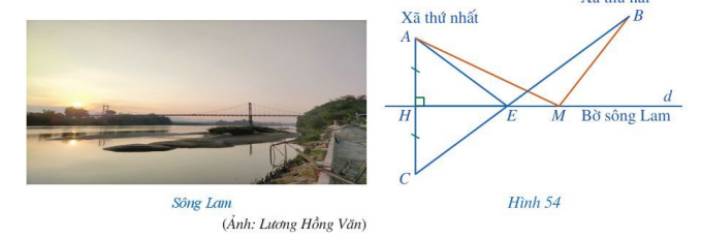
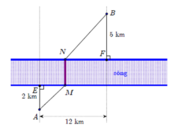
Ta có: HA = HC, \(EH \bot AC\). Vậy EH là đường trung trực của AC nên EA = EC (tính chất đường trung trực của đoạn thẳng).
Tương tự ta có: MH là đường trung trực của AC nên MA = MC.
Xét tam giác MBC: \(BC < MB + MC\)(Trong một tam giác, tổng của hai cạnh luôn lớn hơn độ dài cạnh còn lại).
Ta có:
\(BC < MB + MC = MB + MA\). (1)
Ba điểm B, E, C thẳng hàng nên \(EB + EC = BC\). (2)
Thay (2) vào (1) ta được: \(\begin{array}{l}BC < MB + MA\\EB + EC < MA + MB\end{array}\)
Mà EA = EC nên \(EA + EB < MA + MB\). Vậy bạn Nam nói đúng và khi đó để tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất thì E là vị trí của cây cầu.

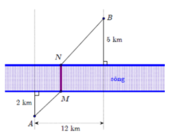
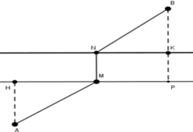
- Vì khoảng cách giữa hai bờ sống là không đổi , cho nên \(\overrightarrow{MN}=\overrightarrow{u}\).
- Tìm A’ là ảnh của A qua phép tịnh tiến theo \(\overrightarrow{u}\). Khi đó AMNA’ là hình bình hành : A’N=AM .
- Do đó : MA+NB ngắn nhất Vì : MA+NB=A’N+NB

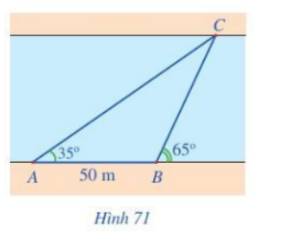
Ta có: \(\widehat C = {65^o} - {35^o} = {30^o}\)(tính chất góc ngoài)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Rightarrow AC = \frac{{AB.\sin B}}{{\sin C}}\)
\( \Leftrightarrow AC = \frac{{50.\sin ({{180}^o} - {{65}^o})}}{{\sin {{30}^o}}} \approx 90,63.\)
Độ rộng của khúc sông là: \(AC.\sin A = 90,63.\sin {35^o} \approx 52\;(m)\)

Xét tam giác ABC, ta có: \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\)
\( \Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}\)
Áp dụng định lí sin trong tam giác BAC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin {37,9^o}}} \approx 40\)
Vậy khoảng cách từ vị trí A đến vị trí B là 40 m.

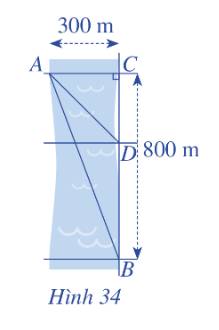
Đổi 300 m =0,3 km, 800 m = 0,8 km
7,2 phút =0,12(h)
Gọi khoảng cách từ C đến D là x (km) (0,8>x>0)
Khi đó, DB=0,8-x (km)
Theo định lý Py-ta-go ta có: \(AD = \sqrt {A{C^2} + C{D^2}} \)\( = \sqrt {0,{3^2} + x^2} \) (km)
Thời gian đi từ A đến D là: \(\frac{{\sqrt {0,{3^2} + x^2} }}{6}\left( h \right)\)
Thời gian đi từ D đến B là: \(\frac{{0,8 - x}}{{10}}\left( h \right)\)
Tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút nên ta có phương trình:
\(\begin{array}{*{20}{l}}
{\frac{{\sqrt {0,{3^2} + {x^2}} }}{6} + \frac{{0,8 - x}}{{10}} = 0,12}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} + 3.\left( {0,8 - x} \right) = 0,12.30}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} - 3x - 1,2 = 0}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} = 3x + 1,2}\\
{ \Rightarrow 25.\left( {0,{3^2} + {x^2}} \right) = {{\left( {3x + 1,2} \right)}^2}}\\
{ \Leftrightarrow 25.\left( {{x^2} + 0,09} \right) = 9{x^2} + 7,2x + 1,44}\\
{ \Leftrightarrow 16{x^2} - 7,2x + 0,81 = 0}\\
{ \Leftrightarrow x = 0,225 \, \, \, (TM)}
\end{array}\)
Vậy khoảng cách từ vị trí C đến D là 225m.

Không gian mẫu là kết quả của việc sắp xếp 10 người theo 1 thứ tự.
⇒ n(Ω) = P10 = 10! = 3 628 800.
a) Gọi M: “A và B đứng liền nhau”
* Coi A và B là một phần tử X.
Số cách xếp X và 8 người khác thành hàng dọc là: 9!
Số cách xếp hai người A và B là: 2!= 2 cách
Theo quy tắc nhân có: 9!.2= 725760 cách xếp thỏa mãn
Xác suất của biến cố M là: 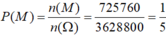
b) Gọi N: “Trong hai người đó có một người đứng ở vị trí số 1 và một người kia đứng ở vị trí cuối cùng”.
+ Sắp xếp vị trí cho A và B: Có 2 cách
+ Sắp xếp vị trí cho 8 người còn lại: có 8! cách
⇒ Theo quy tắc nhân: n(N) = 2.8!
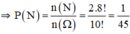






Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)