a/Trong dãy số

Số thứ 2 có 1 chữ số 0 ở phần thập phân

Số thứ 3 có 2 chữ số 0 ở phần thập phân

Số thứ 1000 có 999 chữ số 0 ở phần thập phân

0,0000....1

tự đếm

có 100 số 0

Tổng cộng 5050 số 0.

a) \(n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01\)

\(n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001\)

Như vậy ta có thể điền vào bảng như sau:

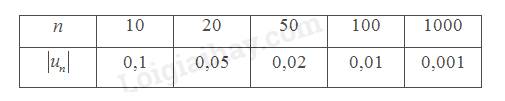
b) \(\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100\)

Vậy \(\left| {{u_n}} \right| < 0,01\) khi \(n > 100\).

\(\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000\)

Vậy \(\left| {{u_n}} \right| < 0,001\) khi \(n > 1000\).

c) Dựa vào trục số ta thấy, khoảng cách từ điểm \({u_n}\) đến điểm 0 trở nên rất bé khi \(n\) trở nên rất lớn.

I. Nội qui tham gia "Giúp tôi giải toán"

1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;

2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.

3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.

Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

đề bài đúng mà em ko cho đè bài linh tinh đâu

a) Xét dãy 

0,1 có 1 số 0 là số thứ 1

0,01 có 2 số 0 là số thứ 2

0,001 có 3 chữ số 0 là số thứ 3 

Vậy số thứ 1000 là 0,0000000........001 (có 1000 chữ số 0 tức bên phải dấu phẩy có 999 chữ số 0 nữa)

b) Từ số thứ nhất đến thứ 100 là:

0,1 ; 0,01 ; 0,001 ; 0,0001 ; ......... ; 0,000.....001 (có 100 chữ số 0)

Mỗi số cần dùng 1 số 1 vậy cần:

1 + 1 + 1 + .... + 1=  1 x 100 = 100 (số 1)

Số thứ nhất cần 1 số 0

Số thứ 2 cần 2 số 0

Số thứ 3 cần 3 số 0

.......................

Số thứ 100 cần 100 số 0

Vậy cần số chữ số 0 là:

1 + 2 + 3 + ... + 100 = 100 x 101 : 2 = 5050 (chữ số 0)

a ) số đó là 0,0001

b ) 20 số 1

     11 số 0

nếu tính thêm 0 thì 12 số 

\(\frac{0,5\cdot\left(0,5+1\right)}{2}=0,375\)

(0,5+0,01):0,01+1=51

51x0,5=26,01

a) Số hạng thứ 1 có 0 số 0 ở phần thập phân

     Số hạng thứ 2 có 1 số 0 ở phần thập phân

     ............................................................

           Số hạng thứ 1000 có 999 số 0 ở phần thập phân

b)  Đầu tiên là cần 100 chữ số 1

     Ở phần nguyên của các số hạng thì có 100 số 0

      + Xét ở phần thập phân:

      Ta viết tổng số chữ số 0 ở phần thập phân thì được:

                         0+1+2+...+99 = (99+0)+(1+98)+...+(47+48) (có 50 cặp)

                                              = 99 x 50 =4950 

Vậy cần 4950+100=5050 chữ số 0

5050 chữ số 0

k mình nha bạn

a) Khoảng cách từ un tới 0 trở nên rất nhỏ (gần bằng 0) khi n trở nên rất lớn

b) Bắt đầu từ số hạng u100 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,01

Bắt đầu từ số hạng u1000 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,001