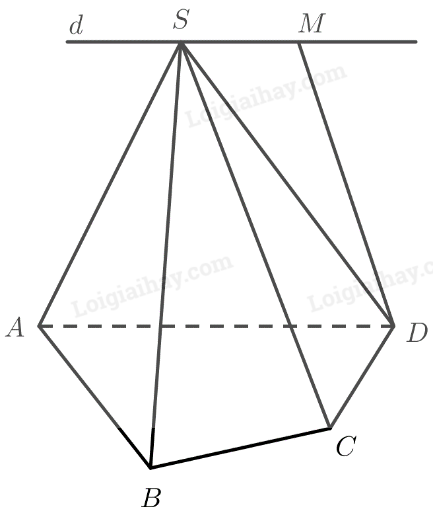
\(A{\rm{D}}M{\rm{S}}\) là hình thang có hai đáy là \(A{\rm{D}}\) và \(M{\rm{S}}\) nên \(A{\rm{D}}\parallel M{\rm{S}}\).

Theo đề bài ta lại có \(d\parallel A{\rm{D}}\).

Do đó \(d \equiv MS\) (theo định lí 1).

Lại có: \(SM \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {SA{\rm{D}}} \right)\).

Ta có: \(MF = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} ,d\left( {M,\Delta } \right) = \left| {y + 1} \right|\).

Xét \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}}  = \left| {y + 1} \right| \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2} \Leftrightarrow {x^2} = 4y \Leftrightarrow y = \frac{1}{4}{x^2}\).

Vậy tập hợp điểm M để \(MF{\rm{ }} = \;d\left( {M,\Delta } \right)\) là parabol \(y = \frac{1}{4}{x^2}\)

a) Đúng

b) Sai

c) Đúng

d) Sai

a) Ta có: \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right|.\left| {\cos \left( {\overrightarrow n ,\overrightarrow {HM} } \right)} \right| = \sqrt {{a^2} + {b^2}} .HM.1 = \sqrt {{a^2} + {b^2}} .HM\)

b) Ta có : \(\overrightarrow n  = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n  \ne 0} \right){\rm{ ,}}\overrightarrow {HM}  = \left( {{x_1} - {x_o};{y_1} - {y_o}} \right) \Rightarrow \overrightarrow n .\overrightarrow {HM}  = a\left( {{x_o} - {x_1}} \right) + b\left( {{y_o} - {y_1}} \right) = a{x_o} + b{y_o} + c\) trong đó \(a{x_1} + b{y_1} = c\).

c) Ta có: \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right|.\left| {\cos \left( {\overrightarrow n ,\overrightarrow {HM} } \right)} \right| \Leftrightarrow \left| {a{x_o} + b{y_o} + c} \right| = \sqrt {{a^2} + {b^2}} .HM \Rightarrow HM = \frac{{\left| {a{x_o} + b{y_o} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Gọi \(M\left( {x;y} \right)\)

Ta có: \(\overrightarrow {AM}  = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow n  = \left( {a;b} \right)\)

\( M \in \Delta \Leftrightarrow \overrightarrow {AM}  \bot \overrightarrow n \)

Hay \(\overrightarrow {AM} .\overrightarrow n  = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0\) (ĐPCM).

a) Tọa độ vecto pháp tuyến của \(\Delta \) là:  

Tọa độ vecto chỉ phương của \(\Delta \) là:

b) Chọn \(x = 0;x = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {0;1} \right),B\left( {1;2} \right)\)

Xét hệ phương trình gồm phương trình của d và \({\Delta _1}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\3x - 2y + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = \frac{3}{2}\end{array} \right.\)

Vậy d và \({\Delta _1}\) cắt nhau tại 1 điểm duy nhất.

Xét hệ phương trình gồm phương trình của d và \({\Delta _2}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\x + 2y + 2 = 0\end{array} \right.\).  Hệ phương trình vô nghiệm.

Vậy d và \({\Delta _2}\) song song với nhau

Xét hệ phương trình gồm phương trình của d và \({\Delta _3}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\2x + 4y--4{\rm{ }} = {\rm{ }}0\end{array} \right.\). Hệ phương trình vô số nghiệm.

Vậy d và \({\Delta _3}\) trùng nhau.

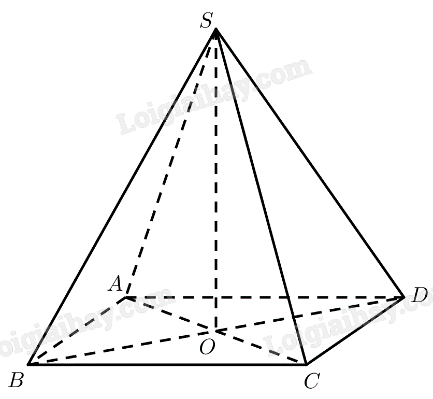
a) \(ABCD\) là hình vuông \( \Rightarrow AC = B{\rm{D}} = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 2 \)

Xét \(\Delta ASC\) có: \(S{A^2} + S{C^2} = 2{a^2} = A{C^2},SA = SC\)

Vậy tam giác \(ASC\) là tam giác vuông cân tại \(S\).

Xét \(\Delta BSD\) có: \(S{B^2} + S{D^2} = 2{a^2} = B{{\rm{D}}^2},SB = SD\)

Vậy tam giác \(BSD\) là tam giác vuông cân tại \(S\).

b) \(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow SO \bot AC\)

\(\Delta BSD\) vuông cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)

\( \Rightarrow SO \bot \left( {ABCD} \right)\)

c) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)

\(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow \widehat {SAO} = {45^ \circ }\)

Vậy \(\left( {SA,\left( {ABCD} \right)} \right) = {45^ \circ }\).

Ta có \({\Delta _1}\)có vecto pháp tuyến là \(\overrightarrow {{n_1}}  = \left( {1;3} \right)\).

Phương trình tổng quát của \({\Delta _2}\) là \(3x - y + 1 = 0\), suy ra \(\overrightarrow {{n_2}}  = \left( {3; - 1} \right)\)

Do \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 1.3 + 3.\left( { - 1} \right) = 0\). Vậy hai đường thẳng vuông góc với nhau.

Cách 2: 

Gọi \(\varphi \) là góc giữa hai đường thẳng, ta có:

\(\cos \varphi  = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {1.3 + 3.( - 1)} \right|}}{{\sqrt {{1^2} + {3^2}} .\sqrt {{3^2} + {{( - 1)}^2}} }} = 0\)

Do đó góc giữa \({\Delta _1}\) và \({\Delta _2}\) là \(\varphi =90^o\)