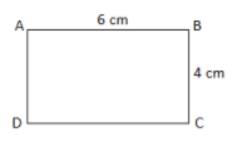
-Vẽ đoạn thẳng AB=6cm và đoạn thẳng AD=4cm vuông góc với nhau.

-Qua B vẽ đường thẳng vuông góc với AB.

-Qua D vẽ đường thẳng vuông góc với AD.Hai đường thẳng này cắt nhau ở C.

=> ABCD là hình chữ nhật cần vẽ

Ve chieu dai AB dai 6cm. ve canh BC dai 4cm. ke CD song song va bang AB . 

ê

Tham khảo:

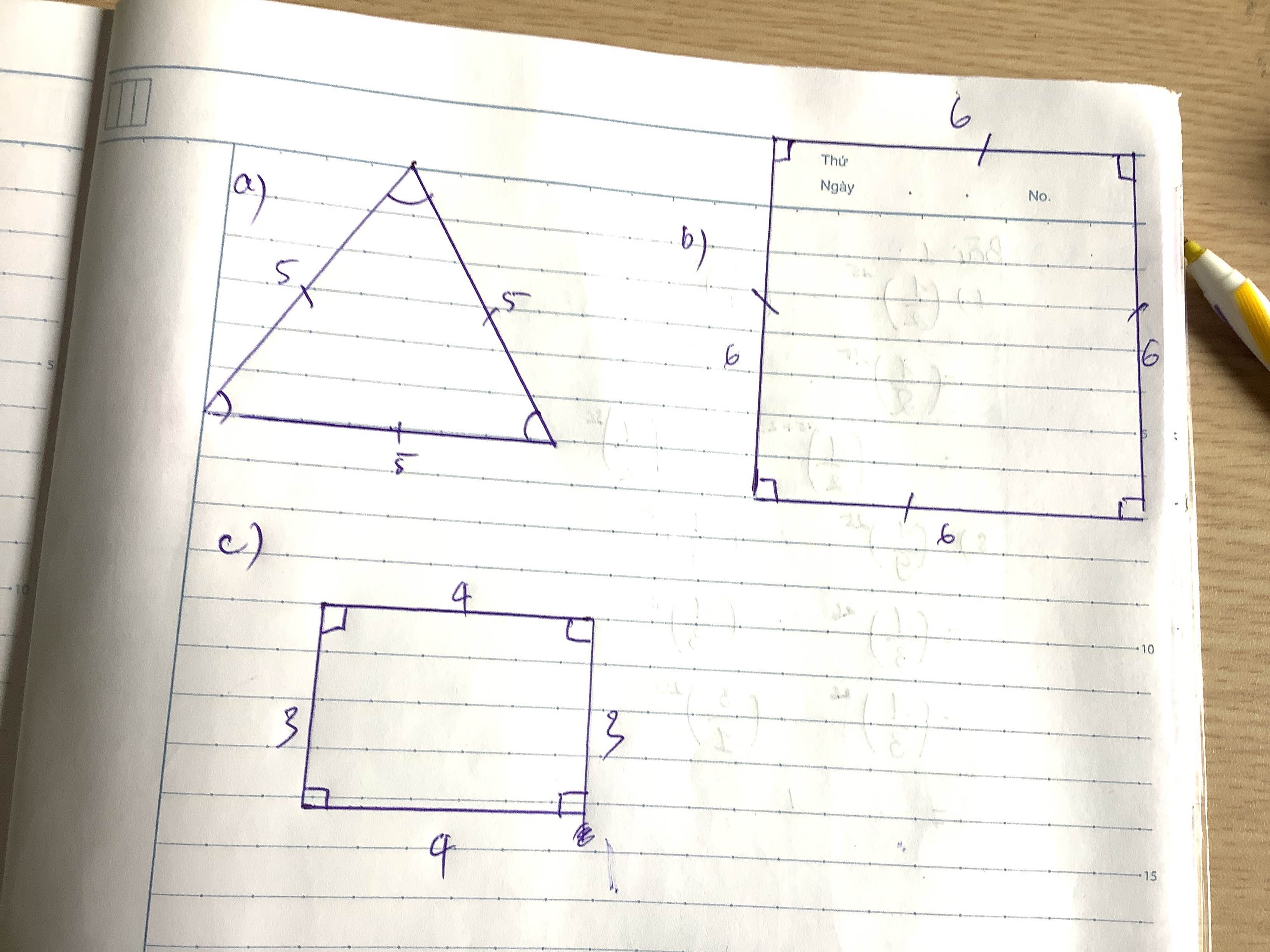
a)

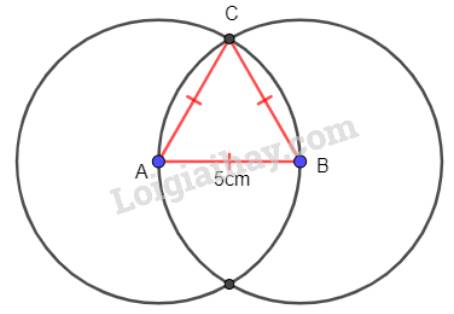
- Kẻ đoạn thẳng AB=5cm.

- Dùng compa vẽ 2 đường tròn bán kính 5cm có tâm lần lượt là A và B.

- Điểm C là giao điểm của hai đường tròn đó.

ABC là tam giác đều cần vẽ.

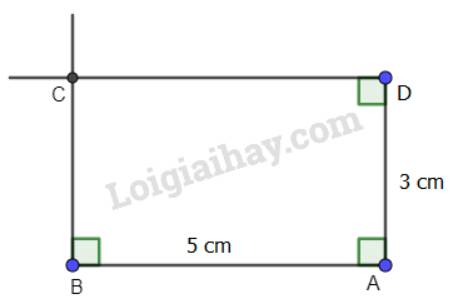
b)

- Vẽ đoạn thẳng AB=5cm và đoạn thẳng AD=3cm vuông góc với nhau.

- Qua B kẻ đường thẳng vuông góc với AB.

- Qua D kẻ đường thẳng vuông góc với AD.

- Hai đường thẳng này cắt nhau ở C.

ABCD là hình chữ nhật cần vẽ.

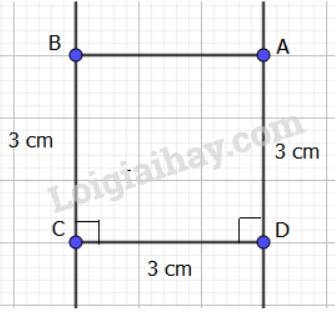
c)

- Vẽ đoạn thẳng CD dài 3cm.

- Vẽ hai đường thẳng vuông góc với CD tại C và D như hình vẽ.

- Trên đường thẳng qua C lấy đoạn thẳng CB=3cm; trên đường thẳng qua D lấy đoạn thẳng DA=3cm.

- Nối 2 điểm A và B ta được hình vuông cần vẽ.

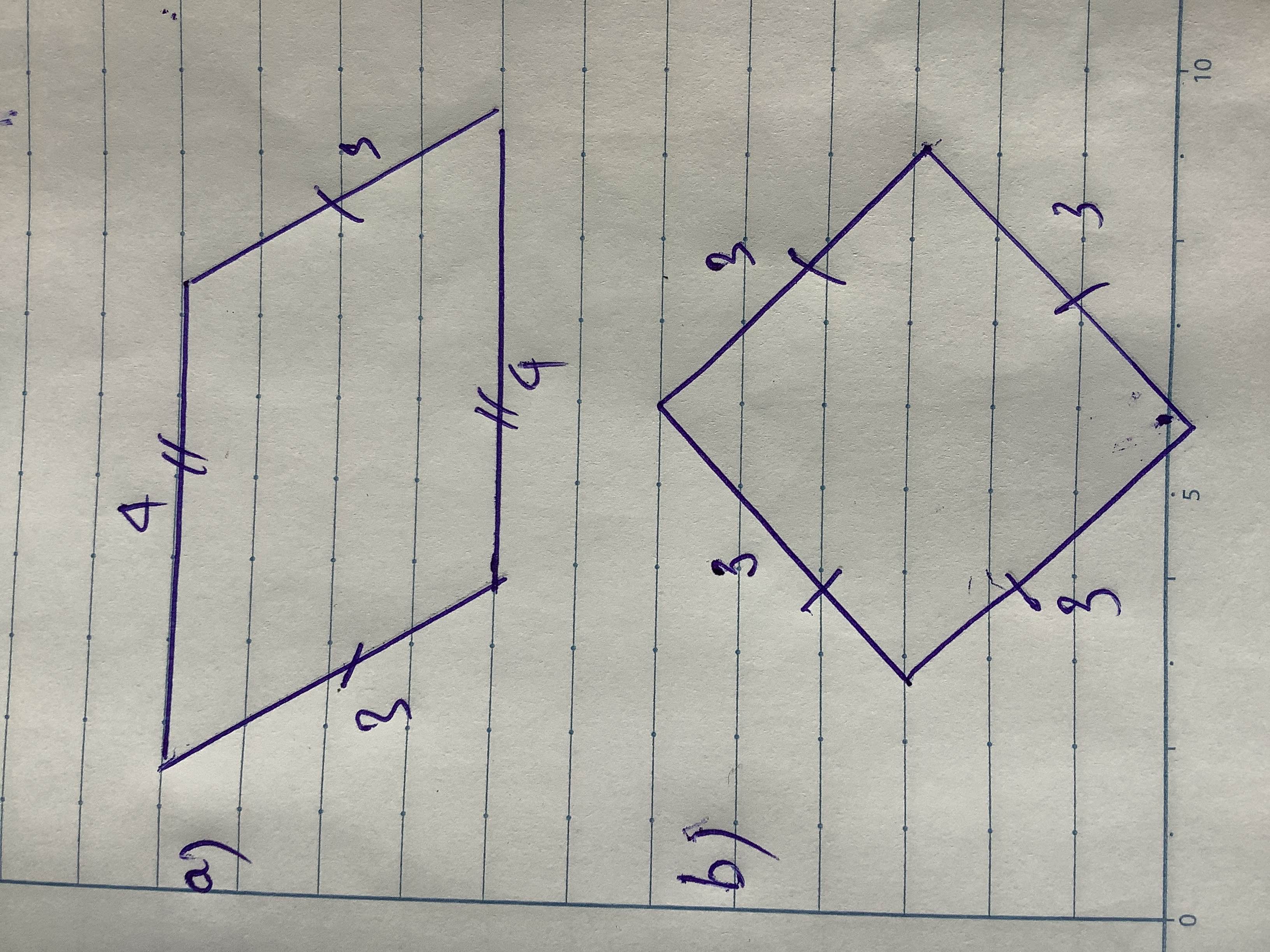
d)

- Vẽ đoạn thẳng AB=6cm.

- Vẽ đường tròn tâm A bán kính 8cm.

- Qua A kẻ đường thẳng vuông góc với AB. Trên đường thẳng lấy H sao cho AH=4cm.

- Qua H kẻ đường thẳng vuông góc với AH cắt đường tròn tại điểm D (chọn 1 trong 2 giao điểm).

- Qua B kẻ đường thẳng song song với AD.

- Qua D kẻ đường thẳng song song với AB.

- Hai đường thẳng cắt nhau tại C.

ABCD là hình bình hành cần vẽ.

e)

- Vẽ đoạn thẳng AB = 5cm.

- Vẽ đường tròn tâm A bán kính 5 cm. Trên đường tròn này lấy điểm D.

- Từ D vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm C sao cho DC = 5 cm.

- Nối C với B ta được hình thoi ABCD có cạnh 5 cm.

Ta được ABCD là hình thoi cần vẽ.

Chọn A.

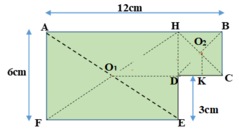
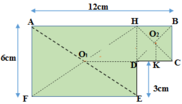
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.

Biểu diễn trọng tâm các bản như hình vẽ sau:

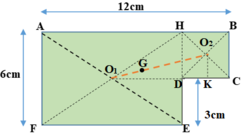
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:

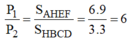
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O 1 O 2 , trong đó  O 1 là trọng tâm của bản AHEF, O 2 là trọng tâm của bản HBCD.

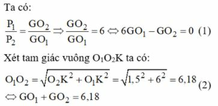
Giải hệ (1) và (2) ta được:  O G 1 = 0,88 c m

Vậy trọng tâm G của bản phẳng nằm trên đoạn  O 1 O 2 cách O 1 một đoạn 0,88 cm.

Chọn A.

Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.

Biểu diễn trọng tâm các bản như hình vẽ sau:

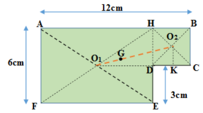
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:

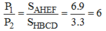
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O₁O₂, trong đó O₁ là trọng tâm của bản AHEF, O₂ là trọng tâm của bản HBCD.

Ta có:

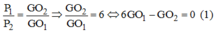
Xét tam giác vuông O₁O₂K ta có:

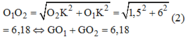
Giải hệ (1) và (2) ta được: GG₁  0,88 cm

Vậy trọng tâm G của bản phẳng nằm trên đoạn O₁O₂ cách O₁ một đoạn 0,88 cm.

cảm ơn bạn nhé

Tham khảo:

a: 

b: