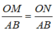1) Cho hình thang ABCD( AB > AD). Hai đường chéo AC và BD cắt nhau tại O. Một đường thẳng tùy ý qua O cắt AB, CD theo thứ tự M,N
a) CMR: OM = ON
b) CMR: DMBN là hình gì ? Vì sao ?
c) CMR: AN// CM
2) Cho tứ giác ABCD có M,N,P,Q lần lượt là trung điểm của AB,BC,CA,AD.
a) CMR: tứ giác MNPQ là hình bình hành
b) Gọi M trung điểm DB. biết AD=6, AB=8. Cho AM= 1/2 DB. Tính QM ?
3) Cho Hình bình hành ABCD( AB>AD) . Kẻ AE, CF lần lượt vuông góc vs BD tại E,F.
a) CMR: AEDF là hình bình hành
b) AE kéo dài cắt CD tại K, CF kéo dài cắt AB tại H. Chứng tỏ rằng AC, BD,HK đồng quy.

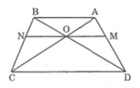
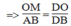 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)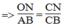 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)