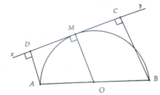
Cho nửa đường tròn (O), đường kính AB. Từ M nằm trên nửa đường tròn, vẽ tiếp tuyến xy với(O). Gọi H và K lần lượt là hình chiếu của A và B trên xy.c/m
a) M là trung điểm HK
b) AB tiếp xúc với đường tròn đường kính HK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

Hướng dẫn, ghét hình học phẳng:
Để ý rằng AB vuông góc (M) tại H nên AH, BH cũng là các tiếp tuyến của (M)
- Nối MA, MB
- \(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn (O) nên suy ra...
- AH, AC là 2 tiếp tuyến \(\Rightarrow\widehat{AMC}=\widehat{AMH}\)
Tương tự: \(\widehat{BMD}=\widehat{BMH}\)
\(\Rightarrow\widehat{CMD}=2\left(\widehat{AMH}+\widehat{BMH}\right)\)
b. AC, AH, BD, BH là các tiếp tuyến nên \(\left\{{}\begin{matrix}AC=AH\\BD=BH\end{matrix}\right.\) \(\Rightarrow AC+BD=...\)
c.
AC song song BD (cùng vuông CD), O và M lần lượt là trung điểm AB, CD
\(\Rightarrow OM\) là đtb hình thang vuông ABDC \(\Rightarrow OM\) vuông CD
Hệ thức lượng tam giác vuông OMK: \(OM^2=OH.OK\)
Mà \(OM=\dfrac{AB}{2}\Rightarrow...\)

1: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO\(\perp\)AB
Gọi G là giao điểm của OM và AB
=>MO vuông góc với AB tại G
\(AM=R\sqrt{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}OG=\dfrac{R^2}{2R}=\dfrac{R}{2}\\GM=2R-\dfrac{R}{2}=\dfrac{3}{2}R\end{matrix}\right.\)
\(\Leftrightarrow AG=\dfrac{R^2\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
\(\left\{{}\begin{matrix}S_{AGM}=S_{BGM}=\dfrac{AG\cdot GM}{2}=\dfrac{R\sqrt{3}}{2}\cdot\dfrac{3R}{2}:2=\dfrac{3R^2\sqrt{3}}{8}\\S_{OGA}=S_{OGB}=\dfrac{OG\cdot GB}{2}=\dfrac{R}{2}\cdot\dfrac{R\sqrt{3}}{2}:2=\dfrac{R^2\sqrt{3}}{8}\end{matrix}\right.\)
\(S_{AOBM}=2\cdot\left(S_{AGM}+S_{OGA}\right)=2\cdot\dfrac{4R^2\sqrt{3}}{8}=R^2\sqrt{3}\)
2: Xét tứ giác NHBI có
\(\widehat{NHB}+\widehat{NIB}=180^0\)
Do đó: NHBI là tứ giác nội tiếp
Suy ra: \(\widehat{NHI}=\widehat{NBA}\)

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA
và DM=DB
nên CD=CA+DB

Ta có ABCD là hình thang vuông tại C và D
Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)
=> AD+BC=2OM=2R. Chú ý rằng CD ≤ AB (hình chiếu đường xiên)
=> S A B C D = 1 2 A D + B C . C D
= R.CD ≤ R.AB = 2 R 2
Do đó S A B C D lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB
a: Xét hình thang AHKB có
O là trung điểm của AB
OM//AHKB
Do đó: M là trung điểm của HK
b: Kẻ MN vuông góc với AB
Xét tứ giác AHMN có \(\widehat{AHM}+\widehat{ANM}=180^0\)
=>AHMN là tứ giác nội tiếp
=>\(\widehat{MAN}=\widehat{MHN}\)
Xét tứ giác MNBK có \(\widehat{MNB}+\widehat{MKB}=180^0\)
=>MNBK nội tiếp
=>\(\widehat{MBN}=\widehat{MKN}\)
Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{NHK}+\widehat{NKH}=90^0\)
=>ΔNKH vuông tại N
ΔNKH vuông tại N có NM là trung tuyến
nên MH=MN
Xét (M) có
MN là bán kính
AB vuông góc MN tại N
Do đó: AB là tiếp tuyến của (M)
=>ĐPCM