cho x, y ,z là các số thực không âm thoả mãn x + y + z = 1. Tính giá trị biểu thức P= √2x2+x+1 + √2y2+y+1 + √2z2+z+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737

Em không chắc đâu nha!
Từ đề bài suy ra \(0\le x;y;z\le1\Rightarrow x\left(1-x\right)\ge0\Rightarrow x\ge x^2\)
Tương tự với y với z.Ta có:
\(P=\sqrt{x^2+x^2+x+1}+\sqrt{y^2+y^2+y+1}+\sqrt{z^2+z^2+z+1}\)
\(\le\sqrt{x^2+2x+1}+\sqrt{y^2+2y+1}+\sqrt{z^2+2z+1}\)
\(=\sqrt{\left(x+1\right)^2}+\sqrt{\left(y+1\right)^2}+\sqrt{\left(z+1\right)^2}\)
\(=\left|x+1\right|+\left|y+1\right|+\left|z+1\right|\)
\(=\left(x+y+z\right)+3=1+3=4\)
Dấu "=" xảy ra khi (x;y;z) = (0;0;1) và các hoán vị của nó.
Vậy....

\(A=\frac{\sqrt{2\left(x+1\right)}}{\sqrt{2}}+\frac{\sqrt{2\left(y+1\right)}}{\sqrt{2}}+\frac{\sqrt{2\left(z+1\right)}}{\sqrt{2}}\le\frac{x+y+z+9}{2\sqrt{2}}=3\sqrt{2}\)
Dấu "=" xảy ra khi \(x=y=z=1\)

\(\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{1}{x+y+z}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{1}{x+y+z}=\frac{y+z+1+x+z+2+x+y-3}{x+y+z}=2\)
\(\Rightarrow\hept{\begin{cases}y+z+1=2x\\x+z+2=2y\\x+y+z=\frac{1}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{5}{6}\\z=-\frac{5}{6}\end{cases}}\)
\(A=2016x+y^{2017}+z^{2017}=2016.\frac{1}{2}+\left(\frac{5}{6}\right)^{2017}+\left(-\frac{5}{6}\right)^{2017}=1008\)
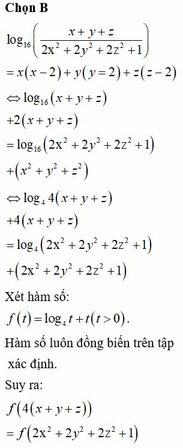


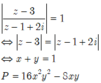
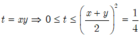
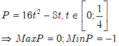
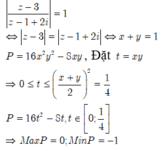
Biểu thức này không có giá trị cụ thể. Bạn xem lại đề.