Cho tam giác ABC đều cạnh 3a . a, Tính| Vectơ AB + Vectơ AC | b, H là trung điểm của BC .Tính|Vectơ CA - Vectơ HC |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
17 tháng 12 2023
Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)
nên 
1 tháng 2 2022
Gọi O là trung điểm của AM
BM=BC/2=a/2
\(\Leftrightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Leftrightarrow MO=\dfrac{a\sqrt{3}}{4}\)
Xét ΔOMB vuông tại M có
\(BO^2=OM^2+BM^2\)
\(=a^2\cdot\dfrac{3}{16}+a^2\cdot\dfrac{1}{4}=a^2\cdot\dfrac{7}{16}\)
\(\Leftrightarrow BO=\dfrac{a\sqrt{7}}{4}\)
Xét ΔBMA có BO là đường trung tuyến
nên \(\overrightarrow{BM}+\overrightarrow{BA}=2\cdot\overrightarrow{BO}\)
\(\Leftrightarrow\left|\overrightarrow{BM}+\overrightarrow{BA}\right|=\dfrac{a\sqrt{7}}{2}\)
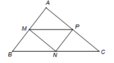
a: Gọi H là trung điểm của BC
Xét ΔABC có AH là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AH}\)
ΔABC đều có AH là đường trung tuyến
nên \(AH=AB\cdot\dfrac{\sqrt{3}}{2}=3a\cdot\dfrac{\sqrt{3}}{2}\)
=>\(2\cdot AH=3a\sqrt{3}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AH=3a\sqrt{3}\)
b:
Gọi I là trung điểm của AH
I là trung điểm của AH
=>\(IA=IH=\dfrac{3a\sqrt{3}}{2}\)
ΔABC đều
mà AH là đường trung tuyến
nên AH vuông góc BC
ΔIHC vuông tại H
=>\(CI^2=HI^2+HC^2\)
=>\(CI^2=\left(\dfrac{3a\sqrt{3}}{2}\right)^2+\left(1,5a\right)^2=9a^2\)
=>CI=3a
\(\left|\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|\)
\(=\left|2\cdot\overrightarrow{CI}\right|=2CI\)
\(=2\cdot3a=6a\)