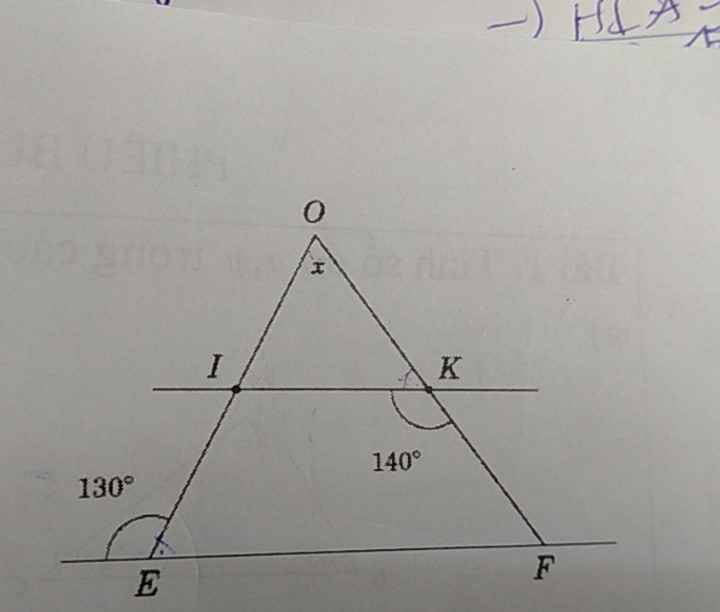
Tính góc x
lm hộ mình, mình đang cần gấp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
∠B₂ = ∠B₁ = 70⁰ (đối đỉnh)
⇒ ∠B₂ = ∠A₁ = 70⁰
Mà ∠B₂ và ∠A₁ là hai góc đồng vị
⇒ a // b

\(\dfrac{x}{27}=\dfrac{5}{9}=>\dfrac{x}{27}=\dfrac{15}{27}=>x=15\)

Ko bạn ơi . Mình làm rồi đây là hình hỏi lại xem các bạn có làm giống mình ko thôi
Bài 1
\(\dfrac{15}{100}=\dfrac{3}{20};\dfrac{25}{200}=\dfrac{1}{8};\dfrac{88}{648}=\dfrac{11}{81};\dfrac{312}{108}=\dfrac{26}{9};\dfrac{8}{1000}=\dfrac{1}{125};\dfrac{27}{315}=\dfrac{3}{35}\)

\(B=\frac{3}{1}+\frac{3}{3}+\frac{3}{6}+...+\frac{3}{210}\)
\(=\frac{6}{2}+\frac{6}{6}+\frac{6}{12}+...+\frac{6}{420}\)
\(=\frac{6}{1.2}+\frac{6}{2.3}+\frac{6}{3.4}+...+\frac{6}{20.21}\)
\(=6\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{20}-\frac{1}{21}\right)\)
\(=6\left(1-\frac{1}{21}\right)\)
\(=6.\frac{20}{21}=\frac{40}{7}\)

a: để \(\dfrac{4}{x}>\dfrac{4}{5}\\ \Rightarrow x< 5\)
mà x là các số tự nhiên
\(\Rightarrow x\in\left\{1;2;3;4\right\}\)
b: để \(\dfrac{1}{9}< \dfrac{x}{9}< \dfrac{4}{9}th\text{ì}1< x< 4\\ \Rightarrow x\in\left\{2;3\right\}\)
A) x>5 => x=1,x=2,x=3,x=4 do hai tử bằng nhau thì phân số nào có mẫu nhỏ hơn sẽ lớn hơn
B) x=2 hoặc x= 3
C) x=7

Minh da ve hinh nhung khong giai duoc phan b nen ban giai ho minh nhe
IK//EF
=>\(\widehat{IKF}+\widehat{OFE}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{OFE}+140^0=180^0\)
=>\(\widehat{OFE}=40^0\)
\(\widehat{IEF}+\widehat{E_1}=180^0\)(hai góc kề bù)
=>\(\widehat{IEF}+130^0=180^0\)
=>\(\widehat{IEF}=50^0\)
Xét ΔOEF có \(\widehat{EOF}+\widehat{FEO}+\widehat{EFO}=180^0\)
=>\(x+50^0+40^0=180^0\)
=>\(x=90^0\)
Lời giải:
Bổ sung điều kiện: $IK\parallel EF$.
Vì $IK\parallel EF$ nên:
$\widehat{OIK}=\widehat{OEF}$ (2 góc đồng vị)
$=180^0-130^0=50^0$
$\widehat{OKI}=180^0-\widehat{IKF}=180^0-140^0=40^0$
Xét tam giác $OIK$ thì:
$x=180^0-(\widehat{OIK}+\widehat{OKI})=180^0-(50^0+40^0)=90^0$