Bài 32. Một người quan sát cao 1m65 nhìn thấy một ống khói theo góc 420 so với phương nằm ngang. Tính chiều cao của ống khói biết người đó đứng cách ống khói 30m. Góc quan sát ống khói sẽ thay đổi như thế nào nếu người đó lùi ra xa thêm 18m nữa.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


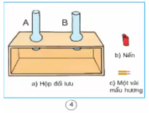
a) Khói hương bay ra qua ống B.
b) Khói hương bay ra từ ống A.
c) Do không khí chuyển động từ nơi lạnh đến nơi nóng, nên khói hương chuyển động sang ống A đang nóng hơn

Bài toán được biểu diễn như hình sau :
Trong đó : AB là chiều cao ống khói
DE là chiều cao của người kia
AC là bóng của ống khói
DC là bóng của người kia
BC là hướng của ánh sáng
Dễ chứng minh ΔABC ~ ΔDEC (g.g)
=> \(\dfrac{AB}{DE}=\dfrac{BC}{EC}=\dfrac{AC}{DC}\)
=> \(AB=\dfrac{AC\cdot DE}{DC}=\dfrac{40,6\cdot1,65}{1,45}=46,2\left(m\right)\)
Vậy chiều cao của ống khói là 46,2m

Diện tích bề mặt được sơn của phần thân ống khói:
\(S=2\pi rh=2\pi\left(\dfrac{0,3}{2}\right).15=0,45\pi\left(m\right)\approx1,414\left(m\right)\)

(Hình ảnh chỉ mang tính chất minh họa)
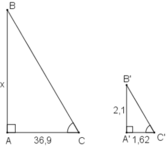
Giả sử thanh sắt là A'B', có bóng là A'C'.
Vì ống khói và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.
Vì cùng một thời điểm nên tia sáng tạo với mặt đất các góc bằng nhau
Vậy chiều cao ống khói là 47,83m.

- Phần trong ống A có không khí nóng vì có 1 ngọn nến đang cháy ở dưới.
- Phần trong ống B có không khí lạnh.
- Khói từ cây hương sẽ bay vào ống A.
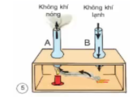
Xét \(\Delta ECD\) vuông tại `E`
Ta có:\(Tan\widehat{D}=\dfrac{EC}{ED}\left(tslg\right)\)
\(\Rightarrow Tan42^o=\dfrac{EC}{30}\\ \Rightarrow EC=30\cdot Tan30^o\\ \Rightarrow EC\approx27m\)
Chiều cao của ống khói đó là:
\(AC=EC+EA\\ \Rightarrow AC=27+1,65\approx28,65m\)
Xét \(\Delta CED\) vuông tại `E`
Ta có: \(Tan\widehat{D}=\dfrac{EC}{ED}\left(tslg\right)\)
\(\Rightarrow Tan\widehat{D}=\dfrac{28,65}{18+30}\\ \Rightarrow Tan\widehat{D}\approx30^o50'.\)