(1,5 điểm) Cho hình vẽ.
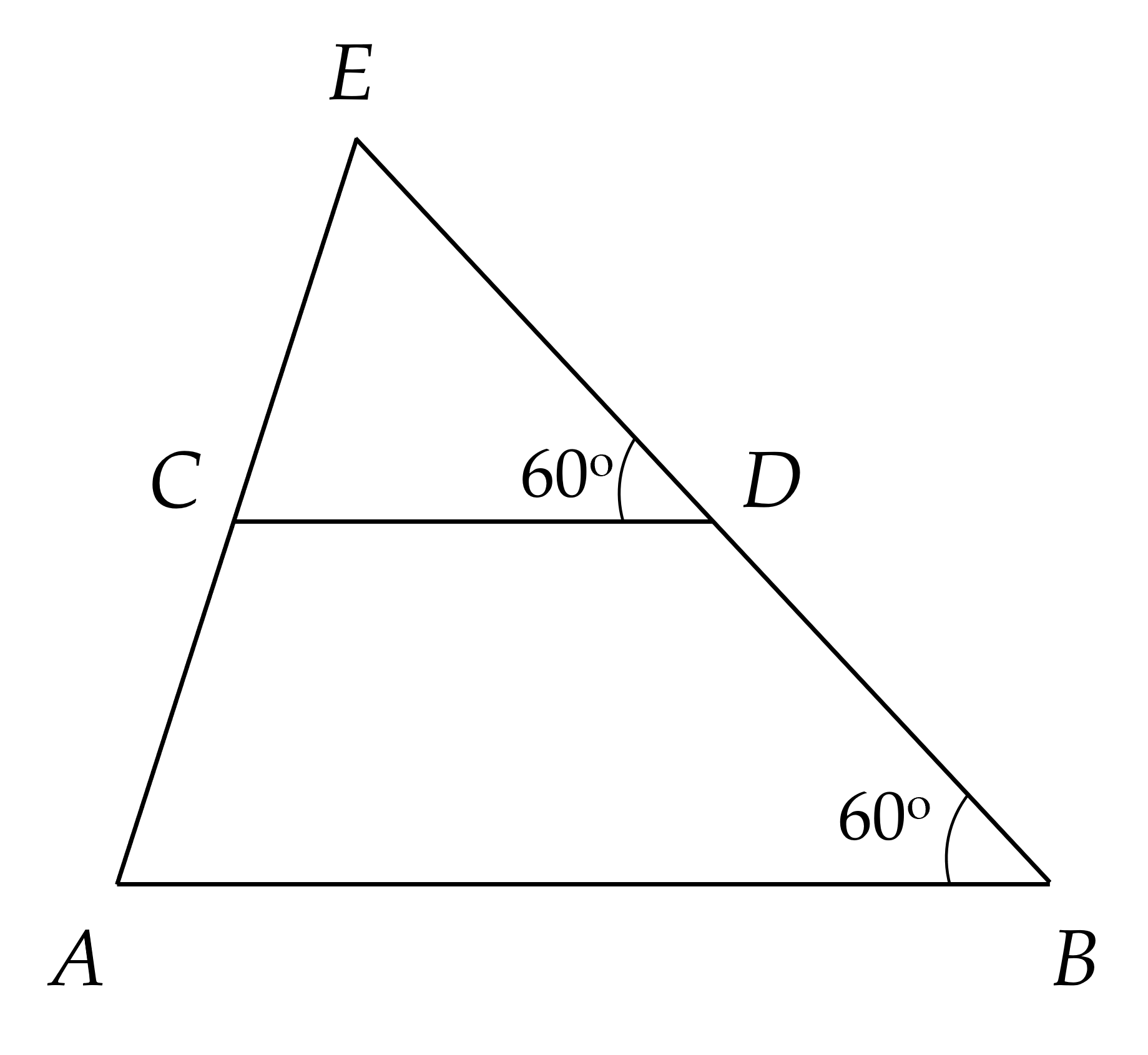
a) Chứng minh $AB // CD$.
b) Chứng minh $\widehat{ACD} + \widehat{BAC} = 180^{\circ}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)

a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)

Không spam nha. Chương trình game xin tặng chương trình học online. Nhằm mục đích game được nhiều người chơi.
Thay mặt người đào tạo chương trình hôm nay : Có 200 suất học bỗng cho những học sinh tích cực hoạt động từ bây giờ ( Mỗi suất học bỗng là 100k). Nhận thưởng bằng cách vào google tìm kiếm.
Link như sau vào google hoặc cốc cốc để tìm kiếm:
https://lazi.vn/quiz/d/17912/game-lien-quan-mobile-ra-doi-vao-ngay-thang-nam-nao
Copy cũng được nha
Bạn hack nick mình thu ib dưới vs nha giúp mk chuyện này
Hình

a) Ta có: CD//Ey
\(\Rightarrow\widehat{CBE}=\widehat{E_1}=130^0\)(so le trong)
b) Ta có: Ta có: CD//Ey
\(\Rightarrow\widehat{EBD}+\widehat{E_1}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{EBD}=180^0-\widehat{E_1}=50^0\)
Ta có: \(\widehat{EBD}+\widehat{B_1}=50^0+40^0=90^0\)
=> AB⊥BE

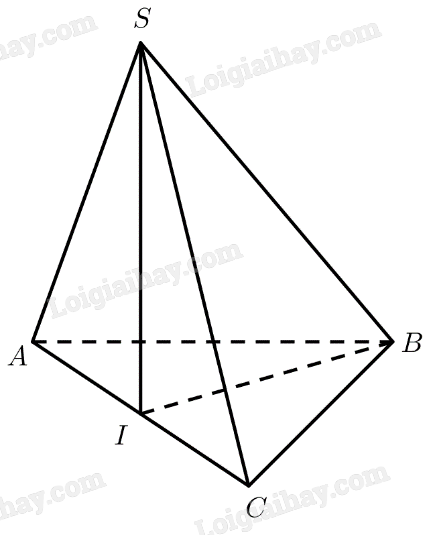
Xét tam giác \(SAC\) có:
\(AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}} = a\sqrt 3 \)
\(SI\) là trung tuyến \( \Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}\)
Ta có: \(S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}\)
\( \Rightarrow \Delta SAI\) vuông tại \(I \Rightarrow SI \bot AC\)
Xét tam giác \(SAB\) vuông tại \(S\) có: \(AB = \sqrt {S{A^2} + S{B^2}} = a\sqrt 2 \)
Xét tam giác \(SBC\) cân tại \(S\) có \(\widehat {BSC} = {60^ \circ }\) nên tam giác \(SBC\) đều. Vậy \(BC = a\)
Xét tam giác \(ABC\) có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(SBI\) có: \(S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}\)
\( \Rightarrow \Delta SBI\) vuông tại \(I \Rightarrow SI \bot BI\)
Ta có:
\(\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)\)

Vì các tia và ở trong góc nên:
(1)
(2)
Từ (1) và (2), suy ra: .
b) Ta có
c) Từ giả thiết, ta có: .
Mà .
Vậy .

Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AEB và DEC có:
\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).
Suy ra: \(\widehat {ABE} = \widehat {DCE}\)
Xét 2 tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {BDC} (= {90^o}\))
\(AB=DC\) (gt)
\(\widehat {ABE} = \widehat {DCE}\) (cmt)
=>\(\Delta AEB = \Delta DEC\)(g.c.g)

Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 70^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 30^\circ \end{array}\)
Xét tam giác ABC và tam giác PMN có:
\(\begin{array}{l}\widehat B = \widehat M = 80^\circ \\\widehat C = \widehat N = 30^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta PMN\) (g-g)
\( \Rightarrow \frac{{AB}}{{PM}} = \frac{{BC}}{{MN}} = \frac{{CA}}{{NP}}\) (Tỉ số đồng dạng)
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰