Trong không gian cho 2006 điểm mà trong đó không có 4 điểm nào đồng phẳng. Người ta nối tất cả các điểm bởi đoạn thẳng. Số nguyên dương \(m\) được gọi là "số tốt" nếu ta có thể gán cho mỗi đoạn thẳng trong các đoạn thẳng đã nối bởi một số tự nhiên không vượt quá \(m\) sao cho mỗi tam giác tạo bởi ba điểm bất kì trong số các điểm đó đều có hai cạnh được gán bởi hai số bằng nhau và cạnh còn lại được gán bởi số lớn hơn hai số đó. Tìm số tốt có giá trị nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Khoảng cách AM là nhỏ nhất khi và chỉ khi M là hình chiếu của A lên mặt phẳng (P).
Ta có AM → = 1 ; − 1 ; 2 là véctơ pháp tuyến của mặt phẳng (P) suy ra AM → là véctơ chỉ phương của đường thẳng AM ⊥ P .
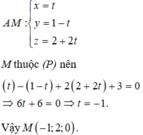

Gọi I là trung điểm A B ⇒ I 5 2 ; 0 ; 5 2 ; AB = 5
M thuộc mặt cầu x - 5 2 2 + y 2 + z - 5 2 2 = 25 4
Tọa độ điểm M là nghiệm của hệ
z = 0 x - 5 2 2 + y 2 + z - 5 2 2 = 25 4
Hạ M H ⊥ A B ; H K ⊥ O x y A B ∥ O x y ⇒ H K = d A B , O x y không đổi mà M H ≥ H K nên S ∆ A B M nhỏ nhất ⇔ MH nhỏ nhất ⇔ M nằm trên đường thẳng ∆ là hình chiếu vuông góc của AB lên mặt phẳng ( Oxy ). Mặt khác (S) tiếp xúc với mặt phẳng ( Oxys ) nên M ∈ ∆
Vậy M 5 2 ; 0 ; 0
Đáp án A

Đáp án B.
Gọi M là điểm thỏa mãn
M A → − 2 M B → + 5 M C → = 0 ⇔ M − 27 4 ; 1 ; 21 4
Khi đó
I A → − 2 I B → + 5 I C → = I M → + M A → − 2 I M → + 5 I M → + 5 M C → = 4 I M → + 0 → = 4 I M →
Biểu thức I A → − 2 I B → + 5 I C → đạt giá trị nhỏ nhất ⇔ I M → nhỏ nhất => I là hình chiếu của M trên mặt phẳng O x z ⇔ I − 27 4 ; 0 ; 21 4 .
Bài toán tổng quát: Trong không gian cho các điểm A 1 , A 2 ,..., A n và mặt phẳng P . Tìm điểm I trên mặt phẳng P sao cho biểu thức k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → đạt giá trị nhỏ nhất, trong đó k 1 , k 2 ,..., k n là những số thực và ∑ i = 0 n k i ≠ 0 .
Cách giải:
- Tìm điểm M thỏa mãn k 1 M A 1 → + k 2 M A 2 → + ... + k n M A n → = 0 .
- Khi đó k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → = ∑ i = 1 n k i I M → .
- Do đó k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → đạt giá trị nhỏ nhất ⇔ I M → nhỏ nhất => I là hình chiếu vuông góc của M trên P .

Chọn A
- Giả sử G là trọng tâm tam giác ABC suy ra G(1;2;1)
- Lấy D(-2;-1;3) ta có C A → = 3 D C →
- Khi đó ta có
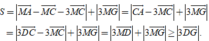
- Vậy S nhỏ nhất khi M là giao điểm của DG với mặt phẳng Oxz Viết phương trình DG và tìm giao điểm ta được M ( - 1 ; 0 ; 7 3 )

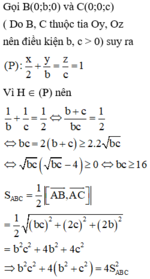

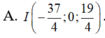
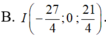
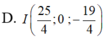
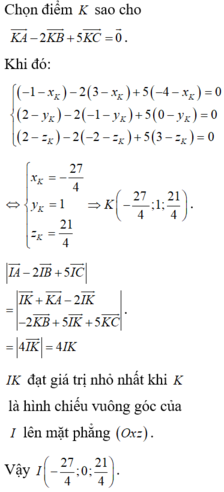
a á ớ
đọc thấy rối quá ạ
(em mới lớp 5 ạ)
chúc mn giải đc nha